Условие задачи:
Заряды по 0,1 мкКл расположены на расстоянии 6 см друг от друга. Найти напряженность в точке, удаленной на 5 см от каждого из зарядов. Оба заряда положительные.
Задача №6.2.23 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(q=0,1\) мкКл, \(l=6\) см, \(r=5\) см, \(E-?\)
Решение задачи:
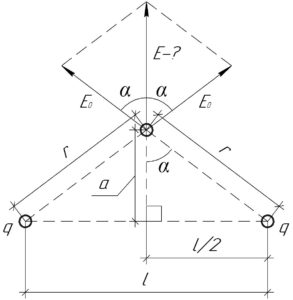Модуль напряженности поля \(E_0\), создаваемого каждым зарядом \(q\) на расстоянии \(r\), найдём по известной формуле:
\[{E_0} = \frac{{kq}}{{{r^2}}}\;\;\;\;(1)\]
Коэффициент \(k\) – это табличная величина, равная 9·109 Н·м2/Кл2.
На схеме к решению видно, что искомая результирующая напряженность поля \(E\) равна сумме проекций напряженностей \(E_0\) на вертикаль, то есть:
\[E = 2{E_0}\cos \alpha \;\;\;\;(2)\]
Вы получите такой же результат, если примените теорему косинусов и тригонометрические преобразования, но этот путь гораздо длиннее. Косинус угла \(\alpha\) равен (смотрите схему):
\[\cos \alpha = \frac{a}{r}\]
Прилежащий катет \(a\) найдем по теореме Пифагора:
\[a = \sqrt {{r^2} – \frac{{{l^2}}}{4}} = \frac{{\sqrt {4{r^2} – {l^2}} }}{2}\]
Тогда имеем:
\[\cos \alpha = \frac{{\sqrt {4{r^2} – {l^2}} }}{{2r}}\;\;\;\;(3)\]
Подставим в формулу (2) выражения (1) и (3):
\[E = \frac{{2kq}}{{{r^2}}} \cdot \frac{{\sqrt {4{r^2} – {l^2}} }}{{2r}}\]
\[E = \frac{{kq\sqrt {4{r^2} – {l^2}} }}{{{r^3}}}\]
Задача решена в общем виде, осталось только посчитать ответ.
\[E = \frac{{9 \cdot {{10}^9} \cdot 0,1 \cdot {{10}^{ – 6}} \cdot \sqrt {4 \cdot {{0,05}^2} – {{0,06}^2}} }}{{{{0,05}^3}}} = 576000\;В/м = 576\;кВ/м\]
Ответ: 576 кВ/м.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
6.2.22 В однородном электрическом поле напряженностью 40 кВ/м, направленным
6.2.24 Одинаковые по модулю, но разные по знаку заряды 40 нКл расположены
6.2.25 В серединах всех сторон равностороннего треугольника расположены одинаковые
проекцию напряженности E0 на вертикаль можно найти из простого соотношения Е0/Е=5/4 ( 4- это высота треугольника)
Являются ли мои рассуждения верными или в задачах с другими условиями будут затруднения?
Рассуждения верные. В задачах с другими численными данными скорее всего будут затруднения по вполне понятным причинам: в этой задаче высота имеет красивое численное значение из-за того, что длины сторон треугольника, образованного искомой высотой, катетом \(\frac{l}{2}\) и гипотенузой \(r\), образуют Пифагорову тройку.
Есть случай, когда заряды разноименные?
Скорее всего нету. Задача от этого не становится сложней, решайте, используя ту же логику
А почему в ответе получается кВ/м, разве Е измеряется не в Н/Кл?
А всё, разобрался.
Правильны оба варианта, но лучше писать В/м.
здравствуйте, я не поняла откуда взялась формула E=2Eo*cosa
Потому что искомая результирующая напряженность поля E равна сумме проекций напряженностей E_0 на вертикаль, то есть E=2E_0*cos a.
Можете пойти другим путем и применить теорему косинусов для равнобедренного треугольника (две стороны которого – это векторы E0, а третья – искомый вектор E, причем угол между векторами E0 равен (180° – 2a)) – получите то же самое.
а разве не (180-2а) ?
Точно, исправил!