Условие задачи:

Расстояние между точечными зарядами 10 и -1 нКл равно 1,1 м. Найти напряженность поля в точке на отрезке, соединяющем заряды, в которой потенциал равен нулю.

Задача №6.3.12 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(q_1=10\) нКл, \(q_2=-1\) нКл, \(l=1,1\) м, \(\varphi=0\), \(E-?\)

Решение задачи:

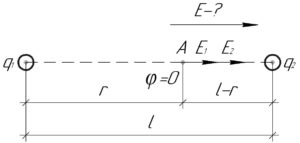Пусть точка, в которой потенциал поля равен нулю (точка A на схеме), находится на расстоянии \(r\) от заряда \(q_1\). Тогда расстояние от этой точки до заряда \(q_2\) равно \(\left( {l — r} \right)\). В таком случае потенциалы полей, создаваемых каждым зарядом в точке A, соответственно равны:

\[\left\{ \begin{gathered}
{\varphi _1} = \frac{{k{q_1}}}{r} \hfill \\
{\varphi _2} = \frac{{k{q_2}}}{{l — r}} \hfill \\
\end{gathered} \right.\]

Коэффициент пропорциональности \(k\) равен 9·10⁹ Н·м²/Кл².

Известно, что потенциал — это скалярная величина, поэтому потенциал суммарного поля в точке A \(\varphi\) найдём следующим образом:

\[\varphi = {\varphi _1} + {\varphi _2}\]

Тогда имеем:

\[\varphi = \frac{{k{q_1}}}{r} + \frac{{k{q_2}}}{{l — r}}\]

В условии задачи сказано, что \(\varphi=0\), поэтому:

\[\frac{{k{q_1}}}{r} + \frac{{k{q_2}}}{{l — r}} = 0\]

\[\frac{{k{q_1}}}{r} = \frac{{ — k{q_2}}}{{l — r}}\]

\[\frac{{{q_1}}}{r} = \frac{{ — {q_2}}}{{l — r}}\]

\[{q_1}l — {q_1}r = — {q_2}r\]

\[{q_1}l = \left( {{q_1} — {q_2}} \right)r\]

\[r = \frac{{{q_1}l}}{{{q_1} — {q_2}}}\;\;\;\;(1)\]

Отлично, мы выразили неизвестное расстояние \(r\) через известные величины. Также найдём \(\left( {l — r} \right)\):

\[l — r = l — \frac{{{q_1}l}}{{{q_1} — {q_2}}}\]

\[l — r = \frac{{ — {q_2}l}}{{{q_1} — {q_2}}}\;\;\;\;(2)\]

Искомая напряженность поля \(E\) равна векторной сумме напряженностей полей, создаваемых каждым зарядом, то есть (смотрите схему):

\[E = {E_1} + {E_2}\]

Модули напряженностей полей \(E_1\) и \(E_2\), создаваемых зарядами \(q_1\) и \(q_2\) в точке A, можно найти по формулам:

\[\left\{ \begin{gathered}
{E_1} = \frac{{k{q_1}}}{{{r^2}}} \hfill \\
{E_2} = \frac{{k\left| {{q_2}} \right|}}{{{{\left( {l — r} \right)}^2}}} \hfill \\
\end{gathered} \right.\]

Учитывая (1) и (2) и раскрывая модуль (\(\left| {{q_2}} \right| = — {q_2}\), так как \({q_2}<0\)), эти формулы примут вид:

\[\left\{ \begin{gathered}
{E_1} = \frac{{k{q_1}{{\left( {{q_1} — {q_2}} \right)}^2}}}{{q_1^2{l^2}}} \hfill \\
{E_2} = \frac{{ — k{q_2}{{\left( {{q_1} — {q_2}} \right)}^2}}}{{q_2^2{l^2}}} \hfill \\
\end{gathered} \right.\]

\[\left\{ \begin{gathered}
{E_1} = \frac{{k{{\left( {{q_1} — {q_2}} \right)}^2}}}{{{q_1}{l^2}}} \hfill \\
{E_2} = \frac{{ — k{{\left( {{q_1} — {q_2}} \right)}^2}}}{{{q_2}{l^2}}} \hfill \\
\end{gathered} \right.\]

\[E = \frac{{k{{\left( {{q_1} — {q_2}} \right)}^2}}}{{{q_1}{l^2}}} + \frac{{ — k{{\left( {{q_1} — {q_2}} \right)}^2}}}{{{q_2}{l^2}}}\]

\[E = \frac{{k{{\left( {{q_1} — {q_2}} \right)}^2}}}{{{l^2}}}\left( {\frac{1}{{{q_1}}} — \frac{1}{{{q_2}}}} \right)\]

Мы получили решение задачи в общем виде. Посчитаем ответ:

\[E = \frac{{9 \cdot {{10}^9} \cdot {{\left( {10 \cdot {{10}^{ — 9}} — \left( { — 1 \cdot {{10}^{ — 9}}} \right)} \right)}^2}}}{{{{1,1}^2}}}\left( {\frac{1}{{10 \cdot {{10}^{ — 9}}}} — \frac{1}{{\left( { — 1 \cdot {{10}^{ — 9}}} \right)}}} \right) = 990\;В/м\]

Ответ: 990 В/м.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

6.3.11 Определить разность потенциалов (по модулю) между точками, отстоящими
6.3.13 В двух вершинах равностороннего треугольника со стороной 0,5 м находятся
6.3.14 Капля росы в виде шара получилась в результате слияния 216 одинаковых капелек