Решение: Конденсаторы соединены в батарею, причем C1=C2=2 мкФ, C3=C4=C5=6 мкФ

Условие задачи:

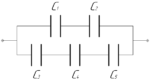Конденсаторы соединены в батарею, причем \(C_1=C_2=2\) мкФ, \(C_3=C_4=C_5=6\) мкФ. Определить напряжение на батарее, если в ней запасена энергия 0,135 Дж.

Задача №6.4.61 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(C_1=C_2=2\) мкФ, \(C_3=C_4=C_5=6\) мкФ, \(W=0,135\) Дж, \(U-?\)

Решение задачи:

Энергию \(W\), запасенную в батарее конденсаторов общей электроемкостью \(C\), можно определить по такой формуле:

\[W = \frac{{C{U^2}}}{2}\]

Откуда искомое напряжение на батарее \(U\) можно найти таким образом:

\[U = \sqrt {\frac{{2W}}{C}} \;\;\;\;(1)\]

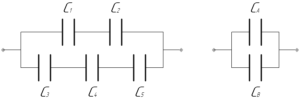
Чтобы определить общую емкость батареи, сначала найдем общую емкость конденсаторов \(C_A\), расположенных на верхней ветви. Поскольку на ней расположены два последовательно соединенных конденсатора одинаковой емкости \(C_1\), то емкость \(C_A\) равна:

\[{C_A} = \frac{{{C_1}}}{2}\]

Аналогично найдем общую емкость конденсаторов \(C_B\), расположенных на нижней ветви. Так как на ней расположены три последовательно соединенных конденсатора одинаковой емкости \(C_3\), то емкость \(C_B\) равна:

\[{C_B} = \frac{{{C_3}}}{3}\]

Так как емкости \(C_A\) и \(C_B\) соединены параллельно между собой, то общую емкость \(C\) легко рассчитать по формуле:

\[C = \frac{{{C_1}}}{2} + \frac{{{C_3}}}{3}\]

\[C = \frac{{3{C_1} + 2{C_3}}}{6}\]

Полученное выражение подставим в формулу (1):

\[U = \sqrt {\frac{{12W}}{{3{C_1} + 2{C_3}}}} \]

Задача решена в общем виде, нам нужно только подставить в итоговую формулу исходные данные и посчитать ответ:

\[U = \sqrt {\frac{{12 \cdot 0,135}}{{3 \cdot 2 \cdot {{10}^{ — 6}} + 2 \cdot 6 \cdot {{10}^{ — 6}}}}} = 300\;В = 0,3\;кВ\]