Условие задачи:
Два точечных заряда 4 и -2 нКл находятся друг от друга на расстоянии 60 см. Определить напряженность поля в точке, лежащей посередине между зарядами.
Задача №6.2.19 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(q_1=4\) нКл, \(q_2=-2\) нКл, \(l=60\) см, \(r=\frac{l}{2}\), \(E-?\)
Решение задачи:
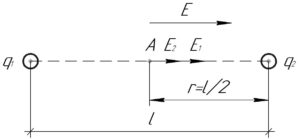Абсолютное значение напряженностей полей \(E_1\) и \(E_2\), создаваемых соответственно зарядами \(q_1\) и \(q_2\), в точке A (смотрите схему к решению), лежащей посередине между зарядами, можно найти по формуле:
\[\left\{ \begin{gathered}
{E_1} = \frac{{k{q_1}}}{{{r^2}}} \hfill \\
{E_2} = \frac{{k\left| {{q_2}} \right|}}{{{r^2}}} \hfill \\
\end{gathered} \right.\]
Здесь \(k\) – коэффициент пропорциональности (из закона Кулона), равный 9·109 Н·м2/Кл2.
По условию точка A посередине между зарядами \(q_1\) и \(q_2\) (то есть \(r=\frac{l}{2}\)). Учитывая это, и раскрывая модуль в нижней формуле, получим:
\[\left\{ \begin{gathered}
{E_1} = \frac{{4k{q_1}}}{{{l^2}}} \hfill \\
{E_2} = \frac{{ – 4k{q_2}}}{{{l^2}}} \hfill \\
\end{gathered} \right.\]
На схеме видно, что напряженности \(E_1\) и \(E_2\) – сонаправлены, поэтому искомую суммарную напряженность \(E\) можно найти по формуле:
\[E = {E_1} + {E_2}\]
Тогда:
\[E = \frac{{4k{q_1}}}{{{l^2}}} + \frac{{ – 4k{q_2}}}{{{l^2}}}\]
\[E = \frac{{4k}}{{{l^2}}}\left( {{q_1} – {q_2}} \right)\]
Произвёдем вычисления:
\[E = \frac{{4 \cdot 9 \cdot {{10}^9}}}{{{{0,6}^2}}}\left( {4 \cdot {{10}^{ – 9}} – \left( { – 2 \cdot {{10}^{ – 9}}} \right)} \right) = 600\;В/м\]
Ответ: 600 В/м.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
6.2.18 Два точечных заряда 4 и 2 нКл находятся друг от друга на расстоянии 50 см. Определить
6.2.20 Найти напряженность поля, создаваемого двумя точечными зарядами 2 и -4 нКл
6.2.21 Определить расстояние между двумя точечными зарядами 16 и -6 нКл, если
Здравствуйте, можете помочь пожалуйста. Два точечных заряда q1 12 нКл и q2 15 нКл находятся в вакууме в вершинах А и D прямоугольника ABCD, длины сторон которого АВ 30 см и ВС 40 см. Определите заряд q0, который перенесли из вершины В в вершину С, если силы электростатического поля совершили работу A = 180 нДж
Помогите решить задачу в трех вершинах квадрата со стороной 5см найти напряженность и потенциал поля 2 мкКл-1,5мкКл и 2.5 мкКл
там явно играет роль принцип суперпозиций.
непонятно как заряд общий найти для плоскости квадрата. (получается просто сложить)
получилось что : f-потенциал W-потенциал энергия q-общий заряд(q1+q2+q3) f=W/q
W=W12+W23+W13 типо складываем потенциальные взаимодействия(влияния) друг с другом.
и получилось что : p-плотность S-площадь квадратика p=q/S q-опять общий.
а E=p/(2*e) 2-потому что плоский конденсатор силовые линии в обе свои стороны eдиэлектрическая проницаемость конст
E=q/(2*S*e)
в конденсатор превращаются эти три точки (как плоскость на 5х5см) потому что подругому незнаю как
Помогите решить задачу в трех вершинах квадрата со стороной 5см найти напряженность и потенциал поля 2 мкКл-1,5мкКл и 2.5 мкКл
Здравствуйте, вы не могли помочь с задачей. В керосине (e=2) на расстоянии 5 см друг от друга находятся два заряда q1=20 нКл и q2=30 нКл. Определить напряженность и потенциал электрического поля в точке, лежащей на перпендикуляре, восстановленном к середине прямой, соединяющей заряды, на расстоянии, равном половине расстояния между зарядами. Изобразить на рисунке.
Здравствуйте. Мне нужна помощь, заранее большое спасибо.
Потенциал поля, созданного точечным зарядом, находящимся в вакууме на расстоянии r = 24 см от него, ф = 2,4 В. Определите модуль напряженности этого поля на расстоянии r, = 12 см от заряда.
Все же просто:\[\varphi = \frac{{kq}}{{{r_1}}}\]Заряд \(q\) равен:\[q = \frac{{\varphi {r_1}}}{k}\]Искомую напряженность найдем следующим образом:\[E = \frac{{kq}}{{r_2^2}}\]Учитывая выражения для заряда \(q\), имеем:\[E = \frac{k}{{r_2^2}} \cdot \frac{{\varphi {r_1}}}{k}\]\[E = \frac{{\varphi {r_1}}}{{r_2^2}}\]Численный ответ равен:\[E = \frac{{2,4 \cdot 0,24}}{{{{0,12}^2}}} = 40\;В/м\]
Нужна помощь, два точечных заряда q1 и q2=-4q1 закреплены на расстоянии 1,2 метра друг от друга. На каком расстоянии от заряда q1 на линии расположения зарядов находится точка с нулевым значением: а)напряженности, б) потенциала поля системы?
задача в трех вершинах квадрата со стороной 5см найти напряженность и потенциал поля 2 мкКл-1,5мкКл и 2.5 мкКл помогите пожалуста
задача в трех вершинах квадрата со стороной 5см найти напряженность и потенциал поля 2 мкКл-1,5мкКл и 2.5 мкКл помогите решить пожалуйста
Срочно нужна помощь, заранее большое спасибо
Электрон без начальной скорости прошел разность потенциалов U0=5 кВ и влетел в горизонтально расположенный плоский конденсатор на равном расстоянии от его пластин. Вектор скорости электрона параллелен пластинам, отстоящим на расстоянии d = 0,5 см. Длина пластин l =5 см. Какую наименьшую разность потенциалов нужно приложить к конденсатору, чтобы электрон не вылетел из него?
Вот же решенная задача, правда численные данные немного отличаются. Но задача решена в общем виде, думаю, пересчитать ответ будет несложно.
Здравствуйте, очень нужна ваша помощь..
Первоначально покоившийся протон, ускоренный электрическим полем напряженностью Е = 1,5∙10^4 В/м и протяженностью 2 м, вылетает из него и подлетает к неподвижному заряду q = 3 мкКл. Чему равна скорость протона на вылете из электрического поля? На каком расстоянии от неподвижного заряда он остановится?
Скорость протона определим из теоремы об изменении кинетической энергии:\[\frac{{m{\upsilon ^2}}}{2} = Eed\;\;\;\;(1)\]Выразим отсюда скорость и посчитаем численный ответ:\[\upsilon = \sqrt {\frac{{2Eed}}{m}} \]\[\upsilon = \sqrt {\frac{{2 \cdot 1,5 \cdot {{10}^4} \cdot 1,6 \cdot {{10}^{ – 19}} \cdot 2}}{{1,6 \cdot {{10}^{ – 27}}}}} = 2,45 \cdot {10^6}\;м/с\]Расстояние, на котором он остановится, от неподвижного заряда будем определять из закона сохранения энергии (кинетическая энергия протона перейдет в потенциальную энергию взаимодействия зарядов):\[\frac{{m{\upsilon ^2}}}{2} = \frac{{kqe}}{r}\]Учитывая равенство (1), имеем:\[Eed = \frac{{kqe}}{r}\]\[Ed = \frac{{kq}}{r}\]Откуда получим:\[r = \frac{{kq}}{{Ed}}\]\[r = \frac{{9 \cdot {{10}^9} \cdot 3 \cdot {{10}^{ – 6}}}}{{1,5 \cdot {{10}^4} \cdot 2}} = 0,9\;м\]
Два протона (с зарядом 1,6*10^-19 Кл) находятся в среде в точках А и В на расстоянии 5 мкм. Найдите напряженность электрического поля в точке С, которая образует вместе с точками А и В равнобедренный прямоугольный треугольник, приврём противолежать гипотенузе (ответ округлите до целых).
Так как точки A и B равноудалены от точки C, то напряженность электрического поля в этой точке, создаваемой каждым из протонов, будет одинакова и равна по модулю:\[{E_0} = \frac{{k{e^2}}}{{{r^2}}}\]Оба вектора \(E_0\) будут перпендикулярны друг другу, поэтому искомую результирующую напряженность поля \(E\) в точке C найдем по теореме Пифагора:\[{E^2} = E_0^2 + E_0^2\]\[{E^2} = 2E_0^2\]\[E = \sqrt 2 {E_0} = \frac{{\sqrt 2 k{e^2}}}{{{r^2}}}\]Для прямоугольного треугольника ABC запишем теорему Пифагора (\(l\) – это длина отрезка AB, \(r\) – длины отрезков AC и BC):\[{l^2} = {r^2} + {r^2}\]\[{l^2} = 2{r^2}\]\[{r^2} = \frac{{{l^2}}}{2}\]Учитывая это, окончательно имеем:\[E = \frac{{2\sqrt 2 k{e^2}}}{{{l^2}}}\]\[E = \frac{{2\sqrt 2 \cdot 9 \cdot {{10}^9} \cdot {{\left( {1,6 \cdot {{10}^{ – 19}}} \right)}^2}}}{{{{\left( {5 \cdot {{10}^{ – 6}}} \right)}^2}}} = 2,6 \cdot {10^{ – 17}}\;В/м\]
в точках A и B, лежащих на одной прямой, на расстоянии 15, находятся два заряда 18 и -28, найти результирующее поле в точках C и D
Интересно, а как догадаться, где находятся точки C и D?
Подскажите, пожалуйста!
Два точечных заряда 27 нКл и -10 нКл находятся в воздухе на расстоянии 10 см.Надо определить напряженность электрического поля в точке А, удалённой от положительного заряда на расстояние 10 см и на 20 см от отрицательного.
Если расположить положительный заряд так, что он будет левее отрицательного, то точка A будет находиться на расстоянии \(l_1=10\) см левее положительного заряда и на расстоянии \(l_2 = l_1 + r =20\) см левее отрицательного заряда. Так как напряженности полей, создаваемых каждым из зарядов, будут противонаправлены, то модуль напряженности результирующего поля будет определять по формуле:\[E = {E_1} – {E_2}\]Здесь \(E_1\) – модуль напряженности электрического поля, создаваемого положительным зарядом, а \(E_2\) – отрицательным зарядом. Тогда: \[E = \frac{{k{q_1}}}{{l_1^2}} – \frac{{k{q_2}}}{{l_2^2}}\]Посчитаем численный ответ:\[E = \frac{{9 \cdot {{10}^9} \cdot 27 \cdot {{10}^{ – 9}}}}{{{{0,1}^2}}} – \frac{{9 \cdot {{10}^9} \cdot 10 \cdot {{10}^{ – 9}}}}{{{{0,2}^2}}} = 22050\;В/м\]При этом вектор напряженности направлен влево
Расстояние между двумя точечными положительными зарядами q1=25 нКл и q2=10 нКл равно 22 см. на каком расстоянии от первого заряда находится точка в которой напряженность поля зарядов равна нулю?
Все просто, нужно решить уравнение:\[E = \frac{{k{q_1}}}{{{r^2}}} – \frac{{k{q_2}}}{{{{\left( {l – r} \right)}^2}}} = 0\]\[\frac{{k{q_1}}}{{{r^2}}} = \frac{{k{q_2}}}{{{{\left( {l – r} \right)}^2}}}\]\[{q_2}{r^2} = {q_1}{\left( {l – r} \right)^2}\]Раскроем квадрат разности в правой части:\[{q_2}{r^2} = {q_1}{l^2} – 2{q_1}lr + {q_1}{r^2}\]\[\left( {{q_1} – {q_2}} \right){r^2} – 2{q_1}lr + {q_1}{l^2} = 0\]\[D = 4q_1^2{l^2} – 4\left( {{q_1} – {q_2}} \right){q_1}{l^2} = 4{q_1}{q_2}{l^2} > 0\]\[r = \frac{{2{q_1}l \pm \sqrt {4{q_1}{q_2}{l^2}} }}{{2\left( {{q_1} – {q_2}} \right)}}\]Окончательно:\[r = \frac{{2{q_1}l \pm 2l\sqrt {{q_1}{q_2}} }}{{2\left( {{q_1} – {q_2}} \right)}}\]\[r = l\frac{{{q_1} \pm \sqrt {{q_1}{q_2}} }}{{{q_1} – {q_2}}}\]Численный ответ равен:\[\left[ \begin{gathered}
r = 0,22 \cdot \frac{{25 \cdot {{10}^{ – 9}} + \sqrt {25 \cdot {{10}^{ – 9}} \cdot 10 \cdot {{10}^{ – 9}}} }}{{25 \cdot {{10}^{ – 9}} – 10 \cdot {{10}^{ – 9}}}} = 0,6 \;м\hfill \\
r = 0,22 \cdot \frac{{25 \cdot {{10}^{ – 9}} – \sqrt {25 \cdot {{10}^{ – 9}} \cdot 10 \cdot {{10}^{ – 9}}} }}{{25 \cdot {{10}^{ – 9}} – 10 \cdot {{10}^{ – 9}}}} = 0,135\;м \hfill \\
\end{gathered} \right.\]
Первый корень нам не подходит, так как точка должна быть между зарядами. Ответ: 13,5 см.
Как решать это же задачу если не дано L?
Не знаю. Пришлите текст задачи, посмотрим как Вам помочь
Здравствуйте, помогите пожалуйста, как решить задачу с условием: точечные заряды q1= 1нКл и q2=-10нКл находятся на расстоянии 55см. Определите величину напряжённости поля в точках прямой, проходящей через заряды, где потенциал поля равен нулю.
Во-первых, сначала нужно найти точки, в которых потенциал поля равен нулю, а их может быть несколько. Для этого изобразите заряд \(q_1\) и заряд \(q_2\), причем первый левее второго. Проверим последовательно три разные точки: слева от заряда \(q_1\), между зарядами и справа от заряда \(q_2\) на условие, что потенциал поля равен нулю. Везде мы примем, что \(r\) – расстояние до заряда \(q_1\).
1) Условие запишется в виде:\[\frac{{k{q_1}}}{r} + \frac{{k{q_2}}}{{l + r}} = 0\]Решая его, Вы получите:\[r = \frac{{ – {q_1}l}}{{{q_2} + {q_1}}} = \frac{{ – 1 \cdot 55}}{{ – 10 + 1}} = 6,11\;см\]Напряженность поля в этой точке будет равна (она направлена влево):\[E = \frac{{k{q_1}}}{{{r^2}}} – \frac{{k\left| {{q_2}} \right|}}{{{{\left( {l + r} \right)}^2}}}\]\[E = \frac{{9 \cdot {{10}^9} \cdot 1 \cdot {{10}^{ – 9}}}}{{{{0,0611}^2}}} – \frac{{9 \cdot {{10}^9} \cdot \left| { – 10 \cdot {{10}^{ – 9}}} \right|}}{{{{\left( {0,55 + 0,0611} \right)}^2}}} = 2170\;В/м\]
2) Условие запишется в виде:\[\frac{{k{q_1}}}{r} + \frac{{k{q_2}}}{{l – r}} = 0\]Решая его, Вы получите:\[r = \frac{{ – {q_1}l}}{{{q_2} – {q_1}}} = \frac{{ – 1 \cdot 55}}{{ – 10 – 1}} = 5\;см\]Напряженность поля в этой точке будет равна (она направлена справо):\[E = \frac{{k{q_1}}}{{{r^2}}} + \frac{{k\left| {{q_2}} \right|}}{{{{\left( {l – r} \right)}^2}}}\]\[E = \frac{{9 \cdot {{10}^9} \cdot 1 \cdot {{10}^{ – 9}}}}{{{{0,05}^2}}} + \frac{{9 \cdot {{10}^9} \cdot \left| { – 10 \cdot {{10}^{ – 9}}} \right|}}{{{{\left( {0,55 – 0,05} \right)}^2}}} = 3960\;В/м\]
3) Условие запишется в виде:\[\frac{{k{q_1}}}{r} + \frac{{k{q_2}}}{{r – l}} = 0\]Решая его, Вы получите:\[r = \frac{{{q_1}l}}{{{q_1} + {q_2}}} = \frac{{1 \cdot 55}}{{1 – 10}} = – 6,11\;см\]Так как \(r < 0\), значит справа от обоих зарядов на прямой, проходящей через заряды, нет такой точки, где потенциал поля равен нулю. К сожалению не могу прикрепить рисунок в комментарии, но текст решения должен быть (по моему мнению) такой
А если уже учли, что заряд отрицательный, почему его значение опять подставляете с минусом?
Вам дали в условии второй заряд со знаком “минус”. Вы в результате решения должны получить формулу, в которую и нужно подставить \(q_2\) со знаком “минус”, этот знак нигде просто так выкидывать нельзя.
Вообще, можно ещё вот так (не раскрывая модуль):
\[E = \frac{{4k{q_1}}}{{{l^2}}} + \frac{{4k\left| {{q_2}} \right|}}{{{l^2}}}\]\[E = \frac{{4k}}{{{l^2}}}\left( {{q_1} + \left| {{q_2}} \right|} \right)\]Ответ, как Вы понимаете, будет такой же
а откуда 9?
Коэффициент пропорциональности (из закона Кулона) \(k\) равен 9·109 Н·м2/Кл2.
Извините, а откуда в формуле перед k 4?
Вообще напряженность определяем так:\[E = \frac{{k{q_1}}}{{{r^2}}}\]Так как \(r = \frac{l}{2}\), то:\[E = \frac{{k{q_1}}}{{{{\left( {\frac{l}{2}} \right)}^2}}} = \frac{{k{q_1}}}{{\frac{{{l^2}}}{4}}} = \frac{{4k{q_1}}}{{{l^2}}}\]
Два точечных заряда по 3 нКл расположены на расстоянии 5см друг от друга. Найти напряжённость электрического поля в точке, находящейся на расстоянии 3 см от положительного заряда и 4 см от отрицательного заряда. Постройте чертеж к задаче.
Напряженности полей от каждого заряда в указанной точке будут перпендикулярны друг другу, поскольку расстояния образуют Пифагорову тройку (3, 4, 5). Поэтому величину напряжённости электрического поля можно найти через теорему Пифагора:\[E = \sqrt {E_1^2 + E_2^2} \]Напряженности \(E_1\) и \(E_2\) найдем по формулам:\[\left\{ \begin{gathered}
{E_1} = \frac{{kq}}{{r_1^2}} \hfill \\
{E_2} = \frac{{kq}}{{r_2^2}} \hfill \\
\end{gathered} \right.\]Тогда:\[E = \sqrt {{{\left( {\frac{{kq}}{{r_1^2}}} \right)}^2} + {{\left( {\frac{{kq}}{{r_2^2}}} \right)}^2}} = kq\sqrt {\frac{1}{{r_1^4}} + \frac{1}{{r_2^4}}} \]\[E = kq\sqrt {\frac{{r_1^4 + r_2^4}}{{r_1^4r_2^4}}} \]\[E = \frac{{kq}}{{r_1^2r_2^2}}\sqrt {r_1^4 + r_2^4} \]Численный ответ равен:\[E = \frac{{9 \cdot {{10}^9} \cdot 3 \cdot {{10}^{ – 9}}}}{{{{0,03}^2} \cdot {{0,04}^2}}}\sqrt {{{0,03}^4} + {{0,04}^4}} \approx 34420\;В/м\]
Чертеж в комментариях прикрепить не могу
Положительный точечный заряд Q1=4·10-9 Кл находится в 3 см от отрицательного Q2=-2·10-9 Кл. Найти потенциал в точке, расположенной в 6 см от Q1 и 5 см от Q2.
Потенциал – величина скалярная, поэтому чтобы узнать потенциал в точке, достаточно сложить потенциалы, создаваемые зарядами в данной точке.\[\varphi = {\varphi _1} + {\varphi _2}\]\[\varphi = \frac{{k{q_1}}}{{{R_1}}} + \frac{{k{q_2}}}{{{R_2}}}\]\[\varphi = \frac{{9 \cdot {{10}^9} \cdot 4 \cdot {{10}^{ – 9}}}}{{6 \cdot {{10}^{ – 2}}}} + \frac{{9 \cdot {{10}^9} \cdot \left( { – 2} \right) \cdot {{10}^{ – 9}}}}{{5 \cdot {{10}^{ – 2}}}} = 600 – 360 = 240\;В\]
Подскажите, а если q1=12, q2=-12, l=10, а r-расположена между зарядами па расстоянии 6см от положительного заряда
\[\left\{ \begin{gathered}
{E_1} = \frac{{k{q_1}}}{{{r^2}}} \hfill \\
{E_2} = \frac{{k\left| {{q_2}} \right|}}{{{{\left( {l – r} \right)}^2}}} \hfill \\
\end{gathered} \right.\]Раскроем модуль, тогда:\[\left\{ \begin{gathered}
{E_1} = \frac{{k{q_1}}}{{{r^2}}} \hfill \\
{E_2} = \frac{{ – k{q_2}}}{{{{\left( {l – r} \right)}^2}}} \hfill \\
\end{gathered} \right.\]
Поскольку напряженности каждого из зарядов сонаправлены, то их результирующая равна:\[E = {E_1} + {E_2}\]\[E = \frac{{k{q_1}}}{{{r^2}}} + \frac{{-k{q_2}}}{{{{\left( {l – r} \right)}^2}}}\]\[E = \frac{{9 \cdot {{10}^9} \cdot 12 \cdot {{10}^{ – 9}}}}{{{{0,06}^2}}} + \frac{{ – 9 \cdot {{10}^9} \cdot \left( { – 12 \cdot {{10}^{ – 9}}} \right)}}{{{{\left( {0,1 – 0,06} \right)}^2}}} = 37500\;В/м = 37,5\;кВ/м\]
Откуда 4 в формуле?
Такой вопрос уже задавали в комментариях, смотрите самый первый вопрос снизу, там я подробно все объяснил
заряд q=4нкл q=-2нкл заряда расположены на расстоянии 60 см друг от друга. Определите напряженность электрического поля E в точке в центре заряда. Если второй заряд тоже положительный, то какова напряженность электрического поля E*?произв
Если выражение “в точке в центре заряда” воспринимать как “в точке, лежащей посередине между зарядами”, то ответ на первый вопрос указан в решении выше.
Найдем ответ на второй вопрос. Если второй заряд будет положительный (то есть \(q_2 = 2\) нКл), то:\[E = {E_1} – {E_2}\]Тогда:\[E = \frac{{4k{q_1}}}{{{l^2}}} – \frac{{4k{q_2}}}{{{l^2}}}\]\[E = \frac{{4k}}{{{l^2}}}\left( {{q_1} – {q_2}} \right)\]Произвёдем вычисления:\[E = \frac{{4 \cdot 9 \cdot {{10}^9}}}{{{{0,6}^2}}}\left( {4 \cdot {{10}^{ – 9}} – 2 \cdot {{10}^{ – 9}}} \right) = 200\;В/м\]
А если 2 -1
\[E = \frac{{4k}}{{{l^2}}}\left( {{q_1}–{q_2}} \right)\]\[E = \frac{{4 \cdot 9 \cdot {{10}^9}}}{{{{0,6}^2}}}\left( {2 \cdot {{10}^{ – 9}}–\left( { – 1 \cdot {{10}^{ – 9}}} \right)} \right) = 300\;В/м\]
Здравствуйте, не могу понять, у меня заряды 4мКл и -4мКл находятся на расстоянии 16 см друг от друга, нужно определить напряженность электрического поля в точке равноудалённой от обоих зарядов на 8 см
Всё, я разобрался)
Здравствуйте. Подскажите, пожалуйста, как решить задачу, если между q1 и q2 точка А, L=4м, Но вот Е1 и Е2 противоположно направлены?
У вас будет так:\[E = {E_1} – {E_2}\]При этом, если заряды положительные (а это так, судя по Вашим словам), то:\[\left\{ \begin{gathered}
{E_1} = \frac{{4k{q_1}}}{{{l^2}}} \hfill \\
{E_2} = \frac{{4k{q_2}}}{{{l^2}}} \hfill \\
\end{gathered} \right.\]
В итоге имеем:\[E = \frac{{4k{q_1}}}{{{l^2}}} – \frac{{4k{q_2}}}{{{l^2}}}\]\[E = \frac{{4k\left( {{q_1} – {q_2}} \right)}}{{{l^2}}}\]Я решал из предположения, что точка A находится посередине между зарядами. Численных значений зарядов Вы не дали, поэтому расчет Вам придется произвести самим.
спасибо большое, вы прямо находка. нигде не могла найти разъяснение или пример конкретно такой задачи!
никак не могу переделать задачу под себя, помогите!! что если нужно найти эту точку где Е=0. мне можно и без вычислений(числа другие потому что)
Смотрите эту задачу
Добрый день!Помогите с это задачей Два точечных заряда 4нкл и 15 нкл расположены на расстоянии 5 см друг от друга. Напряженность электрического поля в точке, находящейся на соединяющий их прямой и удалённой на 2 см от первого заряда и 3 см от второго заряда , равна
Всё же очень просто:\[E = {E_1} – {E_2}\]\[E = \frac{{k{q_1}}}{{r_1^2}} – \frac{{k{q_2}}}{{r_2^2}}\]\[E = \frac{{9 \cdot {{10}^9} \cdot 4 \cdot {{10}^{ – 9}}}}{{{{0,02}^2}}} – \frac{{9 \cdot {{10}^9} \cdot 15 \cdot {{10}^{ – 9}}}}{{{{0,03}^2}}} = – 60000\;В/м = – 60\;кВ/м\]Знак “минус” показывает, что я ошибся с направлением результирующей напряженности (я наобум предположил, что она будет направлена вправо).
А если будет q1=5, q2=-8
\[E = \frac{{4 \cdot 9 \cdot {{10}^9}}}{{{{0,6}^2}}}\left( {5 \cdot {{10}^{ – 9}} – \left( { – 8 \cdot {{10}^{ – 9}}} \right)} \right) = 1300\;В/м\]
Доброго дня!
Есть еще вопрос к этой задаче: Чему равна напряженность электрического поля, если второй заряд положительный?
Тогда у Вас будет так:\[E = {E_1} – {E_2}\]\[E = \frac{{4k{q_1}}}{{{l^2}}} – \frac{{4k{q_2}}}{{{l^2}}}\]\[E = \frac{{4k}}{{{l^2}}}\left( {{q_1} – {q_2}} \right)\]\[E = \frac{{4 \cdot 9 \cdot {{10}^9}}}{{{{0,6}^2}}}\left( {4 \cdot {{10}^{ – 9}} – 2 \cdot {{10}^{ – 9}}} \right) = 200\;В/м\]
подскажите пожалуйста чему будет равна напряженность в той же точки если заряды будут равны 2 и -2 нКл?
Решаете точно также:\[E = \frac{{4k}}{{{l^2}}}\left( {{q_1} – {q_2}} \right)\]\[E = \frac{{4 \cdot 9 \cdot {{10}^9}}}{{{{0,6}^2}}}\left( {2 \cdot {{10}^{ – 9}} – \left( { – 2 \cdot {{10}^{ – 9}}} \right)} \right) = 400\;В/м\]
Добрый день. От чего зависит домножение числителя на 4? От того, величина какого заряда больше?
Конечно же не от этого. Вот у нас есть такая формула:\[{E_1} = \frac{{k{q_1}}}{{{r^2}}}\]При этом я знаю, что \(r = \frac{l}{2}\), подставляю это в формулу, тогда: \[{E_1} = \frac{{k{q_1}}}{{{{\left( {\frac{l}{2}} \right)}^2}}} = \frac{{k{q_1}}}{{\frac{{{l^2}}}{4}}}\] В знаменателе основной дроби у нас появилась другая дробь. Знаменатель этой другой дроби по правилам должен “отправиться” в числитель основной дроби, то есть: \[{E_1} = \frac{{4k{q_1}}}{{{l^2}}}\]
А почему вторая напряжённость с отрицательным знаком?
В моем решении \(E_1\) и \(E_2\) – это модули напряженностей. Заряд \(q_2\) – отрицательный, поэтому модуль \(\left| {{q_2}} \right|\) должен раскрываться со знаком минус, то есть \(\left| {{q_2}} \right| = – {q_2}\).
То есть я в своем решении определил модули напряженностей, на рисунке показал их направление, а потом, спроецировав их на ось, нашел суммарную напряженность (в этой задаче получилось, что она равна сумме напряженностей).