Условие задачи:

Два одинаковых плоских воздушных конденсатора соединены последовательно и подключены к источнику тока. Во сколько раз изменится напряженность электрического поля в одном из них, если другой заполнить диэлектриком с диэлектрической проницаемостью 4?

Задача №6.4.29 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(\varepsilon=4\), \(\frac{E_2}{E_1}-?\)

Решение задачи:

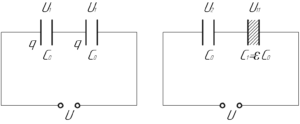Пусть диэлектрик вставляется в первый конденсатор, тогда нам необходимо найти изменение напряженности поля в втором.

Напряженность электрического поля в конденсаторе в общем случае определяется по формуле:

\[E = \frac{U}{d}\;\;\;\;(1)\]

Здесь \(U\) — напряжение между обкладками, а \(d\) — расстояние между ними. Так как расстояние между пластинами второго конденсатора не изменяется, то из формулы (1) видно, что нахождение отношения \(\frac{E_2}{E_1}\) сводится к нахождению отношения напряжений на втором конденсаторе \(\frac{U_2}{U_1}\), то есть:

\[\frac{{{E_2}}}{{{E_1}}} = \frac{{{U_2}}}{{{U_1}}}\;\;\;\;(2)\]

Примем, что напряжение на источнике равно \(U\), и вначале конденсаторы имели одинаковую емкость \(C_0\). Запишем формулу электроемкости для общего случая и выразим из этой формулы заряд \(q\):

\[C = \frac{q}{U}\]

\[q = CU\;\;\;\;(3)\]

Известно, что при последовательном соединении конденсаторов заряд на их обкладках одинаковый. Если воспользоваться формулой (3) и учесть тот факт, что конденсаторы имеют одинаковую емкость \(C_0\), то станет понятно, что напряжение на конденсаторах — одинаковое и равно некоторому \(U_1\). Также известно, что общее напряжение равно сумме напряжений на каждом из конденсаторов, поэтому:

\[U = {U_1} + {U_1}\]

\[U = 2{U_1}\]

\[{U_1} = \frac{U}{2}\;\;\;\;(4)\]

Далее в первый конденсатор вставляют диэлектрик, отчего его емкость увеличивается и становится равной:

\[{C_1} = \varepsilon {C_0}\;\;\;\;(5)\]

Если Вы не уверены в достоверности этой формулы, то можете записать формулу электроемкости плоского конденсатора и убедиться в ней.

Понятно, что напряжения на конденсаторах изменятся. Пусть теперь \(U_{11}\) — разность потенциалов между обкладками первого конденсатора, а \(U_2\) — разность потенциалов между обкладками второго. Проведя аналогичные рассуждения и пользуясь формулой (3), получим такую систему:

\[\left\{ \begin{gathered}
{C_1}{U_{11}} = {C_0}{U_2} \hfill \\
U = {U_{11}} + {U_2} \hfill \\
\end{gathered} \right.\]

Из верхнего равенства системы выразим напряжение \(U_{11}\):

\[{U_{11}} = {U_2}\frac{{{C_0}}}{{{C_1}}}\]

Полученное выражение подставим в нижнее равенство системы:

\[U = {U_2}\frac{{{C_0}}}{{{C_1}}} + {U_2}\]

\[U = {U_2}\frac{{{C_0} + {C_1}}}{{{C_1}}}\]

\[{U_2} = \frac{{U{C_1}}}{{{C_0} + {C_1}}}\]

Принимая во внимание выражение (5), получим:

\[{U_2} = \frac{{\varepsilon U{C_0}}}{{{C_0} + \varepsilon {C_0}}}\]

\[{U_2} = \frac{{\varepsilon U}}{{\varepsilon + 1}}\;\;\;\;(6)\]

Осталось только подставить (4) и (6) в (2):

\[\frac{{{E_2}}}{{{E_1}}} = \frac{{\varepsilon U}}{{\varepsilon + 1}} \cdot \frac{2}{U}\]

\[\frac{{{E_2}}}{{{E_1}}} = \frac{{2\varepsilon }}{{\varepsilon + 1}}\]

Считаем ответ:

\[\frac{{{E_2}}}{{{E_1}}} = \frac{{2 \cdot 4}}{{4 + 1}} = 1,6\]

Ответ: увеличится в 1,6 раза.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

6.4.28 Два конденсатора электроемкостью 4 и 1 мкФ соединены последовательно и подключены
6.4.30 Два одинаковых конденсатора соединены последовательно и подключены к источнику
6.4.31 Бумага пробивается при напряженности поля 18 кВ/см. Два плоских конденсатора с изолятором