Решение: Во сколько раз ускорение свободного падения около поверхности Земли больше

Условие задачи:

Во сколько раз ускорение свободного падения около поверхности Земли больше ускорения свободного падения на высоте, равной трем радиусам Земли?

Задача №2.5.3 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

\(h=3R\), \(\frac{g_1}{g_2}-?\)

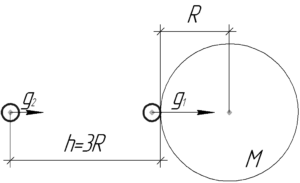Ускорение свободного падения около поверхности Земли легко найти по такой известной формуле:

\[{g_1} = G\frac{M}{{{R^2}}}\]

В этой формуле \(G\) – гравитационная постоянная, \(M\) – масса Земли, а \(R\) – её радиус.

Ускорение свободного падения на некоторой высоте \(h\) от поверхности Земли можно найти по следующей формуле:

\[{g_2} = G\frac{M}{{{{\left( {R + h} \right)}^2}}}\]

По условию \(h=3R\), поэтому:

\[{g_2} = G\frac{M}{{{{\left( {R + 3R} \right)}^2}}} = G\frac{M}{{16{R^2}}}\]

Тогда искомое отношение ускорений свободного падения на разных высотах равно:

\[\frac{{{g_1}}}{{{g_2}}} = \frac{{GM \cdot 16R{}^2}}{{{R^2} \cdot GM}} = 16\]

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.