Условие задачи:

Во сколько раз уменьшится энергия нейтрона \({}_0^1n\) при столкновении с ядром углерода \(C\), если рассеяние произошло на угол 90°? Отношение их масс \({m_c}/{m_n}=12\).

Задача №2.9.3 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(\alpha=90^\circ\), \(\frac{m_c}{m_n}=12\), \(\frac{E_1}{E_2}-?\)

Решение задачи:

Перефразируя вопрос задачи, нам нужно найти отношение начальной кинетической энергии нейтрона к конечной:

\[\frac{{{E_1}}}{{{E_2}}} = \frac{{{m_n}\upsilon _0^2 \cdot 2}}{{2 \cdot {m_n}{\upsilon ^2}}} = \frac{{\upsilon _0^2}}{{{\upsilon ^2}}}\;\;\;\;(1)\]

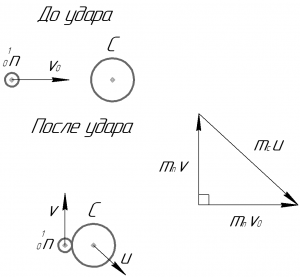
В данном случае мы имеем дело с упругим столкновением нейтрона и углерода. Если рассеяние произошло на прямой угол, значит угол между начальным и конечным направлением движения нейтрона равен 90°. Запишем закон сохранения импульса в векторной форме:

\[\overrightarrow {{m_n}{\upsilon _0}}  = \overrightarrow {{m_n}\upsilon }  + \overrightarrow {{m_c}u}\]

Построим векторный треугольник, соответствующий данному векторному равенству. Видно, что треугольник — прямоугольный, значит по теореме Пифагора справедливо записать:

\[m_c^2{u^2} = m_n^2{\upsilon ^2} + m_n^2\upsilon _0^2\]

\[m_c^2{u^2} = m_n^2\left( {{\upsilon ^2} + \upsilon _0^2} \right)\;\;\;\;(2)\]

Также применим закон сохранения энергии:

\[\frac{{{m_n}\upsilon _0^2}}{2} = \frac{{{m_n}{\upsilon ^2}}}{2} + \frac{{{m_c}{u^2}}}{2}\]

Последний член в правой части данного равенства домножим на \(m_c\), тогда:

\[\frac{{{m_n}\upsilon _0^2}}{2} = \frac{{{m_n}{\upsilon ^2}}}{2} + \frac{{m_c^2{u^2}}}{{2{m_c}}}\]

Домножим обе части на 2 и несколько иначе перепишем равенство:

\[{m_n}\upsilon _0^2 = {m_n}{\upsilon ^2} + \frac{1}{{{m_c}}}m_c^2{u^2}\]

Используя (2), последняя формула примет вид:

\[{m_n}\upsilon _0^2 = {m_n}{\upsilon ^2} + \frac{1}{{{m_c}}}m_n^2\left( {{\upsilon ^2} + \upsilon _0^2} \right)\]

Поделим на \(m_n\), далее раскроем скобки:

\[\upsilon _0^2 = {\upsilon ^2} + \frac{{{m_n}}}{{{m_c}}}\left( {{\upsilon ^2} + \upsilon _0^2} \right)\]

\[\upsilon _0^2 = {\upsilon ^2} + \frac{{{m_n}}}{{{m_c}}}{\upsilon ^2} + \frac{{{m_n}}}{{{m_c}}}\upsilon _0^2\]

Сгруппируем следующим образом, чтобы найти отношение квадратов скоростей:

\[\upsilon _0^2\left( {1 — \frac{{{m_n}}}{{{m_c}}}} \right) = {\upsilon ^2}\left( {1 + \frac{{{m_n}}}{{{m_c}}}} \right)\]

\[\frac{{\upsilon _0^2}}{{{\upsilon ^2}}} = \frac{{1 + \frac{{{m_n}}}{{{m_c}}}}}{{1 — \frac{{{m_n}}}{{{m_c}}}}}\]

Принимая во внимание (1), получается, что мы решили задачу. В условии дано, что \(\frac{m_c}{m_n}=12\), очевидно, что \(\frac{m_n}{m_c}=\frac{1}{12}\).

Посчитаем ответ:

\[\frac{{{E_1}}}{{{E_2}}} = \frac{{1 + \frac{1}{{12}}}}{{1 — \frac{1}{{12}}}} = \frac{{13 \cdot 12}}{{12 \cdot 11}} = 1,18\]

Ответ: в 1,18 раза.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

2.9.2 Шарик массой 100 г упал с высоты 2,5 м на горизонтальную плиту, масса которой
2.9.4 Гранату бросают от поверхности земли под углом 30 градусов к горизонту
2.9.5 Два упругих стальных шара массами m1=0,2 кг и m2=0,1 кг подвешены рядом