Условие задачи:

Во сколько раз период обращения искусственного спутника, совершающего движение по круговой орбите на высоте, равной радиусу Земли, превышает период обращения спутника на околоземной орбите?

Задача №2.5.14 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

$h=R$, $\frac{T_2}{T_1}-?$

Решение задачи:

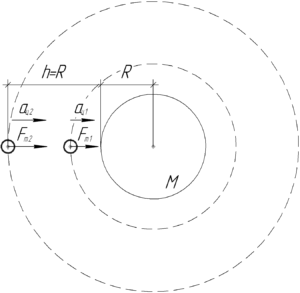Найдем период обращения $T_2$ спутника, движущегося по круговой орбите на высоте $h=R$. Понятно, что сила всемирного тяготения сообщает спутнику центростремительное ускорение $a_ц$, поэтому второй закон Ньютона запишется в следующем виде:

$${F_{т2}} = m{a_{ц2}}\;\;\;\;(1)$$

Сила тяготения определяется законом всемирного тяготения:

$${F_{т2}} = G\frac{{Mm}}{{{{\left( {R + h} \right)}^2}}}\;\;\;\;(2)$$

Чтобы в нашей формуле фигурировал период обращения, нужно выразить через него центростремительное ускорение $a_{ц2}$. Для этого запишем формулу определения ускорения $a_{ц2}$ через угловую скорость и формулу связи последней с периодом.

$${a_{ц2}} = {\omega ^2}\left( {R + h} \right)$$

$$\omega  = \frac{{2\pi }}{T_2}$$

Тогда:

$${a_{ц2}} = \frac{{4{\pi ^2}}}{T_2^2}\left( {R + h} \right)\;\;\;\;(3)$$

Подставим выражения (2) и (3) в равенство (1):

$$G\frac{{Mm}}{{{{\left( {R + h} \right)}^2}}} = \frac{{4{\pi ^2}m\left( {R + h} \right)}}{{{T_2^2}}}$$

$$G\frac{M}{{4{\pi ^2}{{\left( {R + h} \right)}^3}}} = \frac{1}{{{T_2^2}}}$$

$$T_2 = 2\pi \sqrt {\frac{{{{\left( {R + h} \right)}^3}}}{{GM}}}\;\;\;\;(4)$$

Проведем аналогию для спутника, движущегося по околоземной орбите. Понятно, что его период обращения будет равен:

$${T_1} = 2\pi \sqrt {\frac{{{R^3}}}{{GM}}}$$

Теперь подставим в формулу определения периода $T_2$ (в формулу (4)) условие $h=R$:

$${T_2} = 2\pi \sqrt {\frac{{{{\left( {R + R} \right)}^3}}}{{GM}}}  = 2\pi \sqrt {\frac{{8{R^3}}}{{GM}}}$$

Искомое отношение равно:

$$\frac{{{T_2}}}{{{T_1}}} = \sqrt 8  = 2\sqrt 2  = 2,83$$

Ответ: в 2,83 раза.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

2.5.13 Человек на Земле прыгает на высоту 1 м. На какую высоту, совершив ту же работу, он
2.5.15 Определить плотность шарообразной планеты, если вес тела на полюсе в 2 раза больше
2.5.16 На экваторе некоторой планеты тела весят вдвое меньше, чем на полюсе. Плотность