Условие задачи:
В желобе, наклоненном под углом 30° к горизонту и вращающемся с частотой 30 оборотов в минуту вокруг вертикальной оси, проходящей через нижний край желоба, находится шарик. На каком расстоянии от нижнего края желоба остановится шарик?
Задача №2.4.15 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(\alpha=30^\circ\), \(\nu=30\) об/мин, \(l-?\)
Решение задачи:
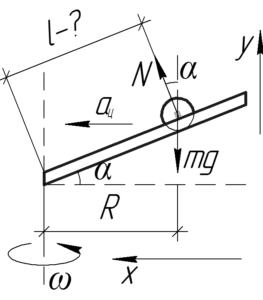 На шарик, находящийся в желобе, действуют сила тяжести \(mg\) и сила реакции опоры \(N\). Шарик не движется вдоль оси \(y\), значит по первому закону Ньютона сумма проекций всех сил на эту ось равна нулю.
На шарик, находящийся в желобе, действуют сила тяжести \(mg\) и сила реакции опоры \(N\). Шарик не движется вдоль оси \(y\), значит по первому закону Ньютона сумма проекций всех сил на эту ось равна нулю.
\[N \cdot \cos \alpha — mg = 0\]
\[N \cdot \cos \alpha = mg\;\;\;\;(1)\]
В горизонтальной плоскости покоящийся относительно желоба шарик описывает окружность какого-то радиуса \(R\). Применим второй закон Ньютона в проекции на ось \(x\):
\[N \cdot \sin \alpha = m{a_ц}\;\;\;\;(2)\]
Запишем формулу определения ускорения \(a_ц\) через угловую скорость \(\omega\), а также формулу связи угловой скорости \(\omega\) с частотой вращения \(\nu\).
\[{a_ц} = {\omega ^2}R\]
\[\omega = 2\pi \nu \]
Тогда имеем:
\[{a_ц} = 4{\pi ^2} {\nu ^2}R\]
Равенство (2) примет вид:
\[N \cdot \sin \alpha = 4{\pi ^2} {\nu ^2}mR\]
Поделим последнее полученное равенство на равенство (1):
\[tg\alpha = \frac{{4{\pi ^2} {\nu ^2}R}}{g}\]
Выразим радиус окружности \(R\), описываемый шариком в горизонтальной плоскости:
\[R = \frac{{g \cdot tg\alpha }}{{4{\pi ^2} {\nu ^2}}}\]
По схеме видно, что справедливо следующее отношение:
\[l = \frac{R}{{\cos \alpha }}\]
В итоге решение задачи в общем виде выглядит так:
\[l = \frac{{g \cdot tg\alpha }}{{4{\pi ^2} {\nu ^2} \cdot \cos \alpha }}\]
Частоту вращения желоба необходимо перевести в систему СИ, далее уже можно считать ответ.
\[30\; об/мин = \frac{{30}}{{60}}\; Гц = 0,5\; Гц\]
\[l = \frac{{10 \cdot tg30^\circ }}{{4 \cdot {{3,14}^2} \cdot {{0,5}^2} \cdot \cos 30^\circ }} = 0,68\; м = 68\; см\]
Ответ: 68 см.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.4.14 Камень, подвешенный к потолку на веревке, движется в горизонтальной плоскости
2.4.16 Гирька массой 0,1 кг, привязанная легкой нерастяжимой нитью, описывает окружность
2.4.17 Груз массой 1 кг, привязанный к нити, отклоняют на 90 градусов от положения
у ВАС ОШИБКА В ФОРМУЛЕ
a центр-ое = 4П^2*V^2*R
А у вас П без квадрата,и,если подставлять по вашей формуле,ответ не сойдется,хотя написан ответ правильный.
Спасибо, решение поправлено! Просто на бумаге я решил её правильно, а при размещении на сайте квадрат перед числом пи был упущен.
l -гипотенуза, она не может быть меньше катета R
Проверьте пожалуйста вычисления
А где написано то, что l меньше R?