Условие задачи:
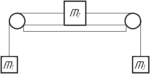Три груза массами \(m_1=1\) кг, \(m_2=2\) кг, \(m_3=3\) кг соединены легкими нитями, проходящими через неподвижные блоки, установленные на краях стола. Коэффициент трения второго тела о стол 0,5. Определите ускорение.
Задача №2.2.2 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(m_1=1\) кг, \(m_2=2\) кг, \(m_3=3\) кг, \(\mu=0,5\), \(a-?\)
Решение задачи:
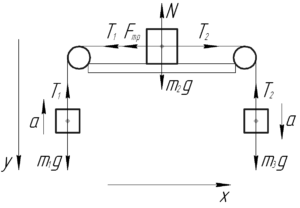Изобразим на схеме все тела и покажем силы, действующие на них. Сначала разберемся со вторым телом. Оно не двигается вдоль оси \(y\), значит по первому закону Ньютона в проекции на эту ось верно записать следующее:
\[N = {m_2}g\;\;\;\;(1)\]
На второе тело действует сила трения скольжения, которая определяется по формуле:
\[{F_{тр}} = \mu N\]
Учитывая (1), получим:
\[{F_{тр}} = \mu {m_2}g\]
Далее силу трения будем подставлять таким полученным выражением.
Так как все грузы двигаются с некоторым одинаковым ускорением, то запишем второй закон Ньютона для каждого груза в проекции на ось, вдоль которой движется каждое тело:
\[\left\{ \begin{gathered}
{m_3}g – {T_2} = {m_3}a \hfill \\
{T_2} – \mu {m_2}g – {T_1} = \hfill \\
{m_1}g – {T_1} = – {m_1}a \hfill \\
\end{gathered} \right.{m_2}a\]
Прибавим к первому выражению системы второе и отнимем третье, после получим:
\[{m_3}g – \mu {m_2}g – {m_1}g = {m_3}a + {m_2}a + {m_1}a\]
\[g\left( {{m_3} – \mu {m_2} – {m_1}} \right) = a\left( {{m_1} + {m_2} + {m_3}} \right)\]
Отсюда искомое ускорение \(a\) равно:
\[a = \frac{{g\left( {{m_3} – \mu {m_2} – {m_1}} \right)}}{{{m_1} + {m_2} + {m_3}}}\]
Посчитаем ответ:
\[a = \frac{{10 \cdot \left( {3 – 0,5 \cdot 2 – 1} \right)}}{{1 + 2 + 3}} = 1,67\; м/с^2\]
Ответ: 1,67 м/с2.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.2.1 Через неподвижный блок перекинута нить с грузами массой 3 и 5 кг. С каким ускорением
2.2.3 Через неподвижный блок перекинута нить, к концам которой подвешены грузы
2.2.4 Два грузика массами m1=0,3 кг и m2=0,2 кг соединены нитью, перекинутой через блок
…в задаче не спрашивается о величине натяжения нитей(!!!)
они – внутренние силы
потому можно сразу написать
(m1 + m2 + m3 ) a = m3 g – m1 g – mu m2 g
a = …
Если нить невесома, это не значит,что Т – const?
Да, в любой точке каждой из нитей сила натяжения одинакова
нить не растяжимая,… и невесомая,…
но имеет силу натяжения
такова сущность марсианских нитей… (если сомневаетесь, обратитесь к Р.Фейнману)
Почему в проекциях на ось,мы отнимаем m3g—T2,а не T2-m3g ?
Потому что ось y на рисунке направлена вниз, из-за этого проекция силы тяжести положительна, а силы натяжения нити – отрицательна.
Можно узнать как найти в этой задаче натяжение нити?
Из первого и последнего уравнений приведённой выше системы можно выразить T_1 и T_2, например:
T_2=m_3*g-m_3*a=m_3*(g-a)
Аналогично можно выразить и силу натяжения T_1
Доброго времени суток,
объясните, почему мы:
Прибавим к первому выражению системы второе и отнимем третье, после получим:
Почему от третьего не вычесть (первое + второе)?
Потому что это одно и тоже, разве что Вы получаете выражения по обе стороны равенства с разными знаками.
У меня:
(1)+(2)-(3)
У Вас:
(3)-((1)+(2))=(3)-(1)-(2)=-((1)+(2)-(3))
Цифры в скобках – это соответствующие выражения.
После получения системы из трёх уравнений – физика заканчивается, и начинается математика. Здесь уже не так важно, как Вы изощряетесь, главное чтобы Вы выразили искомую величину.
Здесь нужно учиться, а не мультики смотреть что ли?
Мы ценим ваше чувство юмора, но сейчас Вы занимаетесь оффтопом.
Нужно или не нужно учиться – решать исключительно Вам.
Я нифига не понимаю , откуда вообще появились эти цифры. Я вообще не понимаю откуда взялась эта задача и вообще эта физика. Да я вообще случной попала на этот сайт, мультики хотела посмотреть!