Условие задачи:

Тело скользит вниз по наклонной плоскости, плавно переходящей в вертикальную круговую петлю радиусом 40 см. Какова должна быть минимальная высота плоскости, чтобы тело не оторвалось в верхней точке петли, если потери на трение составляют 20% от разности потенциальных энергий на верху плоскости и в верхней части петли?

Задача №2.8.43 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(R=40\) см, \(A_{тр}=0,2\Delta E_п\), \(h-?\)

Решение задачи:

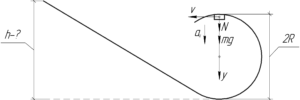Рассмотрим силы, действующие на тело в верхней точке петли — это сила тяжести и сила реакции опоры. Запишем второй закон Ньютона в проекции на ось \(y\):

\[N + mg = m{a_ц}\]

Центростремительное ускорение тела найдем по следующей простой формуле:

\[a_ц = \frac{{{\upsilon ^2}}}{R}\]

\[N + mg = m\frac{{{\upsilon ^2}}}{R}\]

Нужно рассмотреть случай, когда тело не отрывается от петли в верхней точке. Это происходит тогда, когда сила реакции больше нуля. Но чтобы соблюсти условие минимальности высоты плоскости, примем, что сила реакции больше нуля, но бесконечно стремится к ней. Тогда:

\[N \approx 0\]

\[mg = m\frac{{{\upsilon ^2}}}{R}\]

\[{\upsilon ^2} = gR\;\;\;\;(1)\]

Далее воспользуемся законом сохранения энергии, согласно которому работа неконсервативной силы (в нашем случае сила трения) равна изменению полной механической энергии тела.

\[{A_{тр}} = \Delta E\]

В начале у тела была только потенциальная энергия, в верхней точке петли — и потенциальная, и кинетическая. Тогда:

\[{A_{тр}} = \left( {\frac{{m{\upsilon ^2}}}{2} + mg \cdot 2R} \right) — mgh\]

По условию потери на трение (т.е. работа силы трения) составляют 20% от разности потенциальных энергий. Так как работа силы трения отрицательна, то:

\[{A_{тр}} = 0,2\left( {mg \cdot 2R — mgh} \right)\]

Приравняем два полученных выражения для работы силы трения:

\[\left( {\frac{{m{\upsilon ^2}}}{2} + mg \cdot 2R} \right) — mgh = 0,2\left( {mg \cdot 2R — mgh} \right)\]

Подставим ранее полученное выражение (1) в это равенство:

\[\left( {\frac{{mgR}}{2} + 2mgR} \right) — mgh = 0,2\left( {2mgR — mgh} \right)\]

Сократив на \(mg\), получим:

\[\left( {\frac{{R}}{2} + 2R} \right) — h = 0,2\left( {2R — h} \right)\]

\[2,5R — h = 0,4R — 0,2h\]

\[0,8h = 2,1R\]

\[h = \frac{{21R}}{8}\]

Если не переводить радиус петли в систему СИ, то мы получим высоту плоскости в см.

\[h = \frac{{21 \cdot 40}}{8} = 105\; см\]

Ответ: 105 см.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

2.8.42 Пуля массой 10 г подлетает к доске массой 1 кг со скоростью 600 м/с и, пробив ее
2.8.44 В школьном опыте с «мертвой петлей» шарик массой 0,1 кг отпущен с высоты h=3R
2.8.45 Вертикальный невесомый стержень длиной 6 м подвешен одним концом к оси