Условие задачи:
Тело скользит равномерно по наклонной плоскости, угол наклона которой 30°. Определить коэффициент трения тела о плоскость.
Задача №2.3.7 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(\alpha=30^\circ\), \(\mu-?\)
Решение задачи:
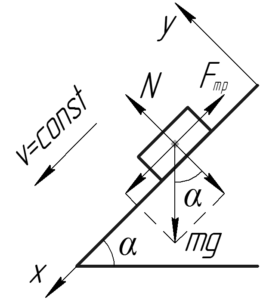 Покажем на схеме наклонную плоскость с телом. Введем оси координат, при это ось \(y\) направим перпендикулярно плоскости, а ось \(x\) — вдоль неё. На тело действуют 3 силы: сила тяжести, сила реакции опоры и сила трения скольжения. Так как тело скользит равномерно по плоскости, то применим первый закон Ньютона в проекции на ось \(x\):
Покажем на схеме наклонную плоскость с телом. Введем оси координат, при это ось \(y\) направим перпендикулярно плоскости, а ось \(x\) — вдоль неё. На тело действуют 3 силы: сила тяжести, сила реакции опоры и сила трения скольжения. Так как тело скользит равномерно по плоскости, то применим первый закон Ньютона в проекции на ось \(x\):
\[mg \cdot \sin \alpha — {F_{тр}} = 0\;\;\;\;(1)\]
Вдоль оси \(y\) тело не движется. Запишем первый закон Ньютона в проекции на ось \(y\):
\[N = mg \cdot \cos \alpha \]
Определим силу трения скольжения по следующей известной формуле:
\[{F_{тр}} = \mu N\]
\[{F_{тр}} = \mu mg \cdot \cos \alpha \]
Последнее подставим в (1), тогда:
\[mg \cdot \sin \alpha — \mu mg \cdot \cos \alpha = 0\]
Откуда получаем такой ответ:
\[\mu = tg\alpha \]
Посчитаем численный ответ к задаче:
\[\mu = tg30^\circ = 0,577\]
Ответ: 0,577.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.3.6 Тело массой 1 кг, имеющее у основания наклонной плоскости скорость 6 м/с
2.3.8 Тело соскальзывает без начальной скорости с наклонной плоскости. Угол наклона
2.3.9 Автомобиль при полностью включенных тормозах (колеса не вращаются) может
Как определить, что ставить, sin или cos?
К сожалению, сложно это объяснить в пару словах и без рисунка. Ищите в интернете информацию по ключевому слову «проекция вектора на ось».
А какой это класс, т.е. задача какого класса
Каким образом, исходя из первого закона Ньютона вы вывели формулу? Не могу понять принцип
Тело движется равномерно и прямолинейно, если векторная сумма всех действующих на него сил равна нулю. Вы записываете эту векторную сумму, а потом проецируете на две оси, так получаете уравнения, благодаря которым Вы можете решить задачу.