Условие задачи:

Тело массы $m$ движется под действием силы $F$. Как изменится модуль ускорения тела, если массу тела уменьшить в два раза, а силу увеличить в два раза?

Задача №2.1.87 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

$m_2=\frac{m_1}{2}$, $F_2=2F_1$, $\frac{a_2}{a_1}-?$

Решение задачи:

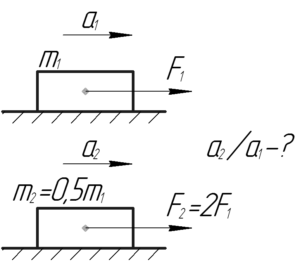Модуль ускорения тела $a$, которое сообщает телу массой $m$ некоторая сила $F$, можно определить из второго закона Ньютона:

$$a = \frac{F}{m}$$

Тогда искомое соотношение ускорений запишется в виде:

$$\frac{{{a_2}}}{{{a_1}}} = \frac{{{F_2} \cdot {m_1}}}{{{m_2} \cdot {F_1}}}$$

Так как по условию $m_2=\frac{m_1}{2}$ и $F_2=2F_1$, то:

$$\frac{{{a_2}}}{{{a_1}}} = \frac{{2{F_1} \cdot {m_1} \cdot 2}}{{{m_1} \cdot {F_1}}} = 4$$

Ответ: увеличится в 4 раза.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

2.1.86 На шероховатой горизонтальной поверхности лежит тело массы 1 кг. Коэффициент
2.1.88 Тело массы m движется под действием двух равных по модулю взаимно
2.1.89 Тело массы 2 кг движется с результирующим ускорением 5 м/с2 под воздействием