Условие задачи:
Тело массой 4 кг вращают в вертикальной плоскости с помощью резинового шнура с частотой 120 об/мин. Найти удлинение и силу натяжения шнура в верхней точке траектории, если его длина в ненапряженном состоянии 30 см, а жесткость 1 кН/м.
Задача №2.4.28 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(m=4\) кг, \(\nu=120\) об/мин, \(l_0=30\) см, \(k=1\) кН/м, \(x-?\), \(F_{упр}-?\)
Решение задачи:
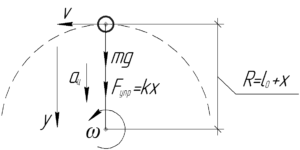Покажем тело, находящееся в положении, указанном в задаче. В этом положении на тело действуют 2 силы: сила тяжести \(mg\), сила натяжения шнура (сила упругости) \(F_{упр}\). Применим второй закон Ньютона в проекции на ось \(y\), тогда:
\[mg + kx = m{a_ц}\;\;\;\;(1)\]
Поскольку в условии дана частота вращения \(\nu\), то необходимо выразить центростремительное ускорение \(a_ц\) через эту частоту. Для этого запишем следующие формулы:
\[{a_ц} = {\omega ^2}R\]
\[\omega = 2\pi \nu \]
Имеем такую формулу:
\[{a_ц} = 4{\pi ^2}{\nu ^2}R\]
Легко заменить, что радиус кривизны траектории \(R\) в верхней точке можно найти, зная начальную длину жгута \(l_0\) и её деформацию \(x\) в этой точке. Важно понимать, что по мере вращения тела длина жгута будет изменяться!
\[R = {l_0} + x\]
\[{a_ц} = 4{\pi ^2}{\nu ^2}\left( {{l_0} + x} \right)\]
Тогда равенство (1) примет такой вид:
\[mg + kx = 4{\pi ^2}{\nu ^2}m\left( {{l_0} + x} \right)\]
Раскроем скобки, все члены с неизвестным \(x\) перенесем в одну сторону, вынесем \(x\) за скобки и выразим его.
\[mg + kx = 4{\pi ^2}{\nu ^2}m{l_0} + 4{\pi ^2}{\nu ^2}mx\]
\[x\left( {k – 4{\pi ^2}{\nu ^2}m} \right) = m\left( {4{\pi ^2}{\nu ^2}{l_0} – g} \right)\]
\[x = \frac{{m\left( {4{\pi ^2}{\nu ^2}{l_0} – g} \right)}}{{k – 4{\pi ^2}{\nu ^2}m}}\]
Вполне очевидно, что силу натяжения шнура \(F_{упр}\) (или силу упругости, что то же самое), можно найти по формуле:
\[{F_{упр}} = kx\]
Перед тем, как подставлять числа в формулу, некоторые из них нужно перевести в систему СИ.
\[120\; об/мин = \frac{{120}}{{60}}\; Гц = 2\; Гц\]
\[30\; см = \frac{{30}}{{100}}\; м = 0,3\; м\]
Считаем ответы:
\[x = \frac{{4 \cdot \left( {4 \cdot {{3,14}^2} \cdot {2^2} \cdot 0,3 – 10} \right)}}{{1000 – 4 \cdot {{3,14}^2} \cdot {2^2} \cdot 4}} = 0,4\; м\]
\[{F_{упр}} = 1000 \cdot 0,4 = 400\; Н\]
Ответ: 0,4 м; 400 Н.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.4.27 Шарик массой 200 г на нити длиной 3 м описывает в горизонтальной плоскости
2.4.29 К потолку лифта на нити длиной 40 см прикреплен шар массой 800 г, который вращается
2.4.30 Какова должна быть максимальная длина выпуклого симметричного относительно