Условие задачи:
Тело массой 100 кг движется по горизонтальной поверхности под действием силы 250 Н, направленной под углом 30° к горизонту и проходящей через центр тяжести тела. Определить коэффициент трения, если тело движется с ускорением 1 м/с2.
Задача №2.1.51 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(m=100\) кг, \(F=250\) Н, \(\alpha=30^\circ\), \(a=1\) м/с2, \(\mu-?\)
Решение задачи:
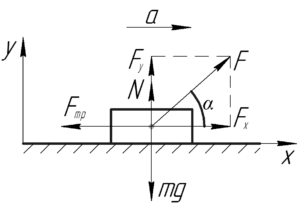Спроецируем все действующие на тело силы на оси координат и запишем законы Ньютона в проекции на эти оси:
\[\left\{ \begin{gathered}
oy:N + F \cdot \sin \alpha – mg = 0 \;\;\;\;(1)\hfill \\
ox:F \cdot \cos \alpha – {F_{тр}} = ma \;\;\;\;(2)\hfill \\
\end{gathered} \right.\]
Сила трения скольжения \(F_{тр}\) определяется по формуле:
\[{F_{тр}} = \mu N\;\;\;\;(3)\]
Из выражения (2) выразим силу трения \(F_{тр}\), а из выражения (1) – силу реакции опоры \(N\).
\[{F_{тр}} = F \cdot \cos \alpha – ma\]
\[N = mg – F \cdot \sin \alpha \]
Полученные формулы подставим в выражение (3), а оттуда уже выразим искомый коэффициент трения \(\mu\).
\[F \cdot \cos \alpha – ma = \mu \left( {mg – F \cdot \sin \alpha } \right)\]
\[\mu = \frac{{F \cdot \cos \alpha – ma}}{{mg – F \cdot \sin \alpha }}\]
Мы получили решение задачи в общем виде. Теперь посчитаем численный ответ.
\[\mu = \frac{{250 \cdot \cos 30^\circ – 100 \cdot 1}}{{100 \cdot 10 – 250 \cdot \sin 30^\circ }} = 0,133\]
Ответ: 0,133.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.1.50 Тело массой 1,5 кг движется вверх по вертикальной стенке под действием силы 20 Н
2.1.52 Тело массой 200 кг упало на грунт со скоростью 100 м/с и погрузилось в него
2.1.53 Брусок массой 50 кг прижимается к вертикальной стенке с силой 100 Н. Какая сила
Зачем вы выражали приложенную силу F, если в решении её не использовали?
Согласно 2 закону Ньютона, вы должны были кроме силы трения по X и силы тяжести
mg совместно с силой опоры N также спроецировать приложенную силу F на ось X и ось Y, а только потом выражать уже коэффициент трения
В данной задаче нужно использовать второй закон Ньютона, который говорит, что сумма всех сил, действующих на тело, равна произведению массы тела на его ускорение:
ΣF = ma
где ΣF – сумма всех сил, m – масса тела, a – ускорение.
Сначала нужно найти горизонтальную и вертикальную составляющие силы:
F_hor = F cos(30°) = 250 * cos(30°) ≈ 216.5 Н
F_ver = F sin(30°) = 250 * sin(30°) ≈ 125 Н
Затем можно найти силу трения, действующую на тело в направлении, противоположном движению:
f_tr = m * a = 100 * 1 = 100 Н
Теперь можно найти коэффициент трения, используя равенство сил трения и нормальной силы:
f_tr = μ * N
N = m * g = 100 * 9.81 ≈ 981 Н
где N – нормальная сила, g – ускорение свободного падения.
Тогда:
μ = f_tr / N = 100 / 981 ≈ 0.102
Ответ: коэффициент трения равен ~0.102.
Подскажите пожалуйста, это же разные задачи и данное решение не походит к моей задачи??? Тело массой 100 кг движется по горизонтальной поверхности под действием силы 250 Н. Направление действия силы образует угол 25° с горизонтом и проходит через центр масс тела. Определите коэффициент трения, если тело движется с ускорением 1 м/с2
почему в проекции на ось oy сумма всех сил равна 0 а в проекции на ось ox = ma
Потому что проекция ускорения тела на ось ox равна \(a\), а на ось oy – нуль.
Численный ответ у меня ни как не получается 1.33
Совпадает ли Ваша конечная формула с моей?
Я пересчитал ответ, у меня опять получилось 0,133.