Условие задачи:

Тело массой 1 кг, брошенное с вышки в горизонтальном направлении со скоростью 20 м/с, через 3 с упало на землю. Какой кинетической энергией обладало тело в момент удара о землю?

Задача №2.7.34 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

$m=1$ кг, $\upsilon_0=20$ м/с, $t=3$ с, $E_к-?$

Решение задачи:

Кинетическую энергию тела $E_к$ можно определить по формуле:

$${E_к} = \frac{{m{\upsilon ^2}}}{2}$$

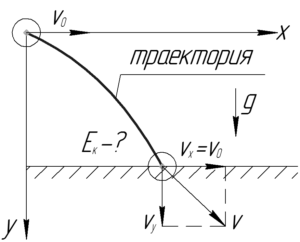
Разложим вектор скорости тела перед ударом $\overrightarrow \upsilon$ на две взаимно перпендикулярные составляющие $\overrightarrow {\upsilon_x}$ и $\overrightarrow {\upsilon_y}$. По теореме Пифагора:

$$\upsilon  = \sqrt {\upsilon _x^2 + \upsilon _y^2}$$

Понятно, что $\upsilon_x$ равна начальной скорости $\upsilon_0$, так как в направлении оси $x$ не действуют никакие силы. Вдоль оси $y$ тело движется равноускоренно с ускорением $g$, поэтому легко найти значение $\upsilon_y$ через время $t$.

$$\left\{ \begin{gathered} {\upsilon _x} = {\upsilon _0} \hfill \\ {\upsilon _y} = gt \hfill \\ \end{gathered} \right.$$

Тогда:

$$\upsilon  = \sqrt {\upsilon _0^2 + {g^2}{t^2}}  \Rightarrow {\upsilon ^2} = \upsilon _0^2 + {g^2}{t^2}$$

$${E_к} = \frac{{m\left( {\upsilon _0^2 + {g^2}{t^2}} \right)}}{2}$$

Посчитаем ответ:

$${E_к} = \frac{{1 \cdot \left( {{{20}^2} + {{10}^2} \cdot {3^2}} \right)}}{2} = 650\;Дж$$

Ответ: 650 Дж.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

2.7.33 Самолет для взлета должен иметь скорость 25 м/с. Длина пробега перед взлетом 100 м
2.7.35 Тепловоз за 5 мин набирает скорость 72 км/ч. Определить среднюю мощность
2.7.36 Укажите график зависимости потенциальной энергии свободно падающего тела