Условие задачи:

Тело брошено вертикально вверх со скоростью 30 м/с. Если принять потенциальную энергию тела в точке бросания равной нулю, то на какой высоте кинетическая энергия тела будет равна половине его потенциальной энергии?

Задача №2.7.56 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

$\upsilon_0=30$ м/с, $E_к=\frac{1}{2}E_п$, $h-?$

Решение задачи:

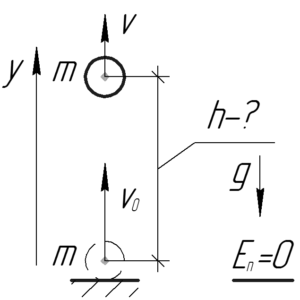В момент бросания у тела имелась только кинетическая энергия. По мере полета кинетическая энергия будет переходить в потенциальную, причем полная механическая энергия тела будет сохраняться по закону сохранения энергии. Поэтому будет верно записать следующее равенство:

$$\frac{{m\upsilon _0^2}}{2} = {E_к} + {E_п}$$

По условию $E_к=\frac{1}{2}E_п$, значит:

$$\frac{{m\upsilon _0^2}}{2} = \frac{1}{2}{E_п} + {E_п}$$

$$\frac{{m\upsilon _0^2}}{2} = \frac{3}{2}{E_п}$$

Если потенциальная энергия в точке бросания равна нулю, то потенциальная энергия $E_п$ определяется по формуле, где $h$ — высота:

$${E_п} = mgh$$

Получим:

$$\frac{{m\upsilon _0^2}}{2} = \frac{3}{2}mgh$$

$$h = \frac{{\upsilon _0^2}}{{3g}}$$

Посчитаем численный ответ:

$$h = \frac{{{{30}^2}}}{{3 \cdot 10}} = 30\;м$$

Ответ: 30 м.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

2.7.55 Камень брошен под углом 60 градусов к горизонту. Как соотносятся между собой
2.7.57 Шарик, подвешенный на нити, качается в вертикальной плоскости так, что его ускорения
2.8.1 Камень массой 1 кг бросили вертикально вверх с начальной скоростью 2 м/с