Условие задачи:
Свинцовый шар массой 500 г, движущийся со скоростью 10 м/с, соударяется с неподвижным шаром из воска массой 200 г, после чего оба шара движутся вместе. Найти кинетическую энергию шаров после соударения.
Задача №2.10.13 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(M=500\) г, \(\upsilon_0=10\) м/с, \(m=200\) г, \(E_к-?\)
Решение задачи:
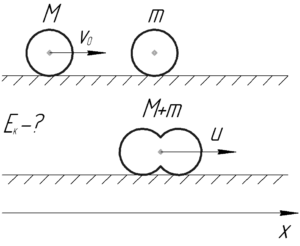 После абсолютно неупругого удара шары слипнутся и будут двигаться с некоторой скоростью \(u\). Понятно, что их кинетическую энергию после удара легко найти по формуле:
После абсолютно неупругого удара шары слипнутся и будут двигаться с некоторой скоростью \(u\). Понятно, что их кинетическую энергию после удара легко найти по формуле:
\[{E_к} = \frac{{\left( {M + m} \right){u^2}}}{2}\;\;\;\;(1)\]
Скорость шаров \(u\) после соударения можно найти из закона сохранения импульса, записанного в проекции на ось \(x\):
\[M{\upsilon _0} = \left( {M + m} \right)u\]
\[u = \frac{{M{\upsilon _0}}}{{M + m}}\]
Таким образом, формула (1) примет вид:
\[{E_к} = \frac{{\left( {M + m} \right)}}{2} \cdot \frac{{{M^2}\upsilon _0^2}}{{{{\left( {M + m} \right)}^2}}}\]
\[{E_к} = \frac{{{M^2}\upsilon _0^2}}{{2\left( {M + m} \right)}}\]
Осталось только посчитать численный ответ, но перед этим переведем массы шаров в систему СИ, то есть переведем из грамм в килограммы.
\[500\; г = \frac{{500}}{{1000}}\; кг = 0,5\; кг\]
\[200\; г = \frac{{200}}{{1000}}\; кг = 0,2\; кг\]
\[{E_к} = \frac{{{{0,5}^2} \cdot {{10}^2}}}{{2\left( {0,5 + 0,2} \right)}} = 17,9\; Дж\]
Ответ: 17,9 Дж.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.10.12 Пушка, стоящая на горизонтальной поверхности, стреляет под углом 30 градусов
2.10.14 Стоящий на льду человек массой 60 кг ловит мяч массой 0,5 кг, который летит
2.10.15 Тележка движется по горизонтальной поверхности со скоростью 0,5 м/с. Её догоняет
Почему нельзя воспользоваться законом сохранения энергии, просто сложив начальные кинетические энергии тел?
Потому что столкновение неупругое, происходит потеря энергии
Игорь все объяснил верно и лаконично