Условие задачи:
Стоящий на льду человек массой 60 кг ловит мяч массой 0,5 кг, который летит горизонтально со скоростью 20 м/с. На какое расстояние откатился человек с мячом, если коэффициент трения равен 0,05?
Задача №2.10.14 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(M=60\) кг, \(m=0,5\) кг, \(\upsilon_0=20\) м/с, \(\mu=0,05\), \(S-?\)
Решение задачи:
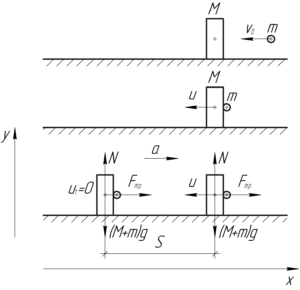На систему “человек – мяч” до удара и сразу после него не действуют горизонтальные силы, поэтому система замкнута вдоль оси \(x\). Это дает нам право воспользоваться законом сохранения импульса (в проекции на ось \(x\)):
\[m{\upsilon _0} = \left( {m + M} \right)u\]
Выразим скорость человека с мячом сразу после удара \(u\):
\[u = \frac{{m{\upsilon _0}}}{{m + M}}\;\;\;\;(1)\]
Далее человек с мячом в руках начнёт равнозамедленное движение, поскольку на него будет действовать сила трения скольжения. Так как вдоль оси \(y\) человек не движется, то запишем первый закон Ньютона в проекции на эту ось:
\[N = \left( {m + M} \right)g\;\;\;\;(2)\]
Силу трения скольжения определяют по такой формуле:
\[{F_{тр}} = \mu N\]
Учитывая (2), имеем:
\[{F_{тр}} = \mu \left( {m + M} \right)g\;\;\;\;(3)\]
Применим второй закон Ньютона уже в проекции на ось \(x\):
\[{F_{тр}} = \left( {m + M} \right)a\;\;\;\;(4)\]
Приравняем правые части (3) и (4) и выразим ускорение \(a\):
\[\left( {m + M} \right)a = \mu \left( {m + M} \right)g\]
\[a = \mu g\;\;\;\;(5)\]
В конце концов человек прекратит своё скольжение, пройдя перед этим расстояние \(S\). В кинематики доказывается, что справедливо следующее:
\[0 – {u^2} = – 2aS\]
\[S = \frac{{{u^2}}}{{2a}}\]
Подставим в последнюю формулу полученные ранее выражения (1) и (5), тогда решим задачу в общем виде:
\[S = \frac{{{m^2}\upsilon _0^2}}{{2\mu g{{\left( {m + M} \right)}^2}}}\]
Посчитаем численный ответ:
\[S = \frac{{{{0,5}^2} \cdot {{20}^2}}}{{2 \cdot 0,05 \cdot 10 \cdot {{\left( {0,5 + 60} \right)}^2}}} = 0,027\; м = 27\; мм\]
Ответ: 27 мм.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.10.13 Свинцовый шар массой 500 г, движущийся со скоростью 10 м/с, соударяется
2.10.15 Тележка движется по горизонтальной поверхности со скоростью 0,5 м/с. Её догоняет
2.10.16 Конькобежец, стоя на льду, бросил вперед гирю массой 5 кг и вследствие отдачи
А как решается задача если нужно найти массу мяча? Я уже понял что ответ 500 грамм будет, но хочу узнать как меняются формулы, а скольжение с мячом равно 0.04м (остальное идентично)
Можно (нужно) из конечной формулы выразить \(m\):\[S = \frac{{{m^2}\upsilon _0^2}}{{2\mu g{{\left( {m + M} \right)}^2}}}\]Из этой формулы имеем:\[{m^2}\upsilon _0^2 = 2\mu gS{\left( {m + M} \right)^2}\]В правой части раскроем квадрат суммы масс:\[{m^2}\upsilon _0^2 = 2\mu gS\left( {{m^2} + 2mM + {M^2}} \right)\]Раскроем скобки:\[{m^2}\upsilon _0^2 = 2\mu gS{m^2} + 4\mu gSmM + 2\mu gS{M^2}\]Мы получили квадратное уравнение относительно искомой массы \(m\):\[\left( {2\mu gS – \upsilon _0^2} \right){m^2} + 4\mu gSMm + 2\mu gS{M^2} = 0\]\[D = 16{\mu ^2}{g^2}{S^2}{M^2} – 8\mu gS{M^2}\left( {2\mu gS – \upsilon _0^2} \right)\]\[D = 8\mu gS{M^2}\upsilon _0^2\]\[m = \frac{{ – 4\mu gSM \pm \sqrt {8\mu gS{M^2}\upsilon _0^2} }}{{2\left( {2\mu gS – \upsilon _0^2} \right)}}\]Корень со знаком “плюс” – лишний, поскольку масса получается отрицательной (знаменатель отрицательный). Окончательно:\[m = \frac{{4\mu gSM + \sqrt {8\mu gS{M^2}\upsilon _0^2} }}{{2\left( {\upsilon _0^2 – 2\mu gS} \right)}}\]Численный ответ посчитаете сами
Кстати, если у нас с Вами отличаются пути \(S\), то и масса \(m\) будет разной (не 0,5 кг).
Божечки спасибо, для меня это задача казалась нерешаемой, готовлюсь к экзамену, и ваш сайт очень помогает.
Если посчитать все на калькуляторе, получается 0.1111111, откуда взялось 0.027?
Вы просто неправильно считаете
в материалах ОГЭ2018 ответ в задаче 1 м
Вероятно представленная задача и Ваша не полностью идентичны