Условие задачи:

Снаряд массой 20 кг, летевший горизонтально, попадает в платформу с песком массой 10 т и застревает в песке. С какой скоростью летел снаряд, если платформа начала двигаться со скоростью 1 м/с?

Задача №2.8.3 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

$m=20$ кг, $M=10$ т, $u=1$ м/с, $\upsilon-?$

Решение задачи:

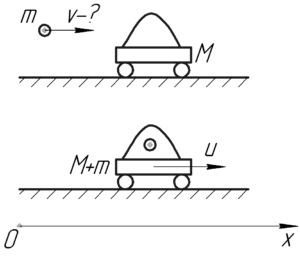Понятно, что описанный в задании процесс прошел очень быстро, поэтому никакие силы (например, сила тяжести) не смогли изменить импульс тел на значительную величину. В таком случае верно записать закон сохранения импульса, хотя система рассматриваемых тел может быть и не замкнута:

$$m\upsilon  = \left( {m + M} \right)u$$

$$\upsilon  = \frac{{\left( {m + M} \right)u}}{m}$$

Переведем массу платформы с песком в единицы системы СИ.

$$10\; т = 10 \cdot {10^3}\; кг = {10^4}\; кг$$

$$\upsilon  = \frac{{\left( {20 + {{10}^4}} \right) \cdot 1}}{{20}} = 501\; м/с = 0,5\; км/с$$

Кстати, в этой задаче мы имеем дело с абсолютно неупругим ударом.

Ответ: 0,5 км/с.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

2.8.2 Найти скорость винтовки при отдаче, если её масса в 500 раз больше массы пули
2.8.4 Тело находится на краю горизонтальной плоскости. Затем этот край плоскости
2.8.5 Какую скорость приобретает ракета массой 2 кг, если продукты горения массой