Условие задачи:
Сколько метров пройдет тело, свободно падая без начальной скорости в течение трех секунд у поверхности планеты, радиус которой меньше земного на одну треть, а средняя плотность планеты на 10% меньше, чем плотность Земли?
Задача №2.5.10 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(R_1=\frac{2}{3}R_з\), \(\rho_1=0,9\rho_з\), \(t=3\) с, \(H-?\)
Решение задачи:
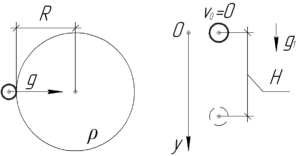 Сначала разберемся как ускорение свободного падения вблизи поверхности некоторой планеты зависит от средней плотности планеты и её радиуса. Для этого запишем всем известную формулу определения:
Сначала разберемся как ускорение свободного падения вблизи поверхности некоторой планеты зависит от средней плотности планеты и её радиуса. Для этого запишем всем известную формулу определения:
\[g = G\frac{M}{{{R^2}}}\;\;\;\;(1)\]
Определить массу планеты, зная её плотность \(\rho\) и объем \(V\), возможно по следующей формуле:
\[M = \rho \cdot V\;\;\;\;(2)\]
Объем сферической планеты определим по формуле:
\[V = \frac{4}{3}\pi {R^3}\;\;\;\;(3)\]
Подставим (3) в (2), а полученное в результате — в формулу (1). Тогда:
\[g = \frac{4}{3}G\pi \rho R\]
Тогда ускорения свободного падения на рассматриваемой планете \(g_1\) и на Земле \(g_з\) можно определить из формул:
\[\left\{ \begin{gathered}
{g_з} = \frac{4}{3}G\pi {\rho _з}{R_з} \hfill \\
{g_1} = \frac{4}{3}G\pi {\rho _1}{R_1} \hfill \\
\end{gathered} \right.\]
Поделим нижнее равенство на верхнее, тогда получим:
\[\frac{{{g_1}}}{{{g_з}}} = \frac{{{\rho _1}{R_1}}}{{{\rho _з}{R_з}}}\]
\[{g_1} = \frac{{{\rho _1}{R_1}}}{{{\rho _з}{R_з}}}{g_з}\]
Поскольку в условии дано, что \(R_1=\frac{2}{3}R_з\) и \(\rho_1=0,9\rho_з\), то:
\[{g_1} = \frac{{0,9{\rho _з} \cdot 2{R_з}}}{{3{\rho _з}{R_з}}}{g_з}\]
\[{g_1} = 0,6{g_з}\;\;\;\;(4)\]
При движении без начальной скорости в поле силы тяжести тело пройдет за время \(t\) расстояние \(H\), определяемое по формуле:
\[H = \frac{{{g_1}{t^2}}}{2}\]
Учитывая (4), имеем:
\[H = 0,3{g_з}{t^2}\]
Посчитаем ответ:
\[H = 0,3 \cdot 10 \cdot {3^2} = 27\; м\]
Ответ: 27 м.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.5.9 На сферической планете вес тела на полюсе в 3 раза больше веса тела на экваторе
2.5.11 Чему равно ускорение свободного падения на высоте, равной половине радиуса
2.5.12 Определить, с каким ускорением падают тела на поверхность Луны, зная, что радиус
там не на радиус меньше не на 2/3 а 1/3
В дано всё записано верно, если радиус планеты R1 меньше земного Rз на одну треть, то R1=2/3Rз.