Условие задачи:

Сила в 6 Н растягивает пружину на 2 см. Какую работу надо произвести, чтобы растянуть пружину на 6 см?

Задача №2.6.11 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

$F=6$ Н, $x_1=2$ см, $x_2=6$ см, $A-?$

Решение задачи:

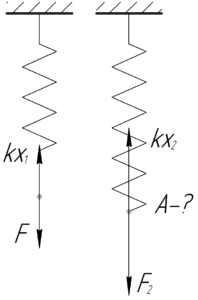Искомую работу $A$ некоторой внешней силы найдем как изменение потенциальной энергии деформации пружины. Так как изначально пружина была не деформирована, а значит её начальная потенциальная энергия была равна нулю, то работа равна конечной потенциальной энергии деформации пружины.

$$A = {E_2}$$

$$A = \frac{{kx_2^2}}{2}\;\;\;\;(1)$$

Сила $F$ растягивает пружины на величину $x_1$, применим закон Гука:

$$F = k{x_1}$$

Выразим неизвестную жесткость $k$:

$$k = \frac{F}{{{x_1}}}$$

Тогда формула (1) примет вид:

$$A = \frac{{Fx_2^2}}{{2{x_1}}}$$

Переведем величины деформаций в систему СИ и посчитаем ответ:

$$2\;см = \frac{2}{{100}}\;м = 0,02\;м$$

$$6\;см = \frac{6}{{100}}\;м = 0,06\;м$$

$$A = \frac{{6 \cdot {{0,06}^2}}}{{2 \cdot 0,02}} = 0,54\;Дж = 540\;мДж$$

Ответ: 540 мДж.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

2.6.10 Тело массой 2 кг тянут по горизонтальной поверхности с помощью пружины, которая
2.6.12 К резинке длиной 50 см привязана гирька массой 20 г. При вращении гирьки
2.6.13 Груз массой 4 кг подвешен на пружине жесткостью 1 кН/м. Определите дополнительную