Условие задачи:

Шоссе имеет вираж с уклоном 10° при радиусе закругления дороги в 100 м. На какую максимальную скорость рассчитан вираж?

Задача №2.4.13 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(\alpha=10^\circ\), \(R=100\) м, \(\upsilon-?\)

Решение задачи:

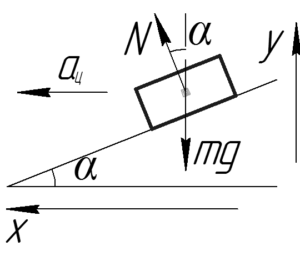Покажем на схеме поперечное сечение виража и автомобиль, находящийся на нём. Покажем все силы, действующие на автомобиль: это сила тяжести \(mg\) и сила реакции опоры \(N\). Так как автомобиль неподвижен в направлении оси \(y\), то запишем первый закон Ньютона в проекции на эту ось:

\[N \cdot \cos \alpha  = mg\;\;\;\;(1)\]

Также применим второй закон Ньютона в проекции на ось \(x\):

\[N \cdot \sin \alpha  = m{a_ц}\;\;\;\;(2)\]

Поделим равенство (2) на равенство (1), тогда:

\[tg\alpha  = \frac{{{a_ц}}}{g}\;\;\;\;(3)\]

Центростремительное ускорение \(a_ц\) легко найти через скорость автомобиля \(\upsilon\) и радиус закругления дороги \(R\):

\[{a_ц} = \frac{{{\upsilon ^2}}}{R}\]

Формула (3) в таком случае примет вид:

\[tg\alpha  = \frac{{{\upsilon ^2}}}{{gR}}\]

Откуда максимальная скорость автомобиля на вираже \(\upsilon\) равна:

\[\upsilon  = \sqrt {gR \cdot tg\alpha } \]

Посчитаем ответ:

\[\upsilon  = \sqrt {10 \cdot 100 \cdot tg10^\circ }  = 13,28\; м/с = 47,8\; км/ч\]

Ответ: 47,8 км/ч.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

2.4.12 Конькобежец движется по закруглению ледяной дорожки радиусом 2,5 м со скоростью
2.4.14 Камень, подвешенный к потолку на веревке, движется в горизонтальной плоскости
2.4.15 В желобе, наклоненном под углом 30 градусов к горизонту и вращающемся с частотой