Условие задачи:
Шарик, подвешенный на нити, качается в вертикальной плоскости так, что его ускорения в крайнем и нижнем положениях равны по модулю друг другу, а сила натяжения в нижнем положении равна \(T\). Угол отклонения нити в крайнем положении равен \(\alpha\). Чему равна масса шарика?
Задача №2.7.57 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(a_1=a_2\), \(T\), \(\alpha\), \(m-?\)
Решение задачи:
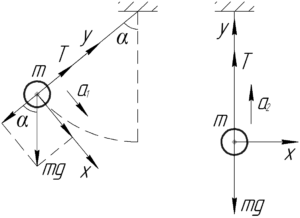Изобразим схему к задаче, на которой покажем крайнее и нижнее положении колеблющегося шарика.
Сначала рассмотрим крайнее положение (часть схемы слева). Чтобы найти ускорение шарика \(a_1\) в этом положении введем ось \(y\) по направлению нити, а ось \(x\) – перпендикулярно ей. Так как в этой точке у шарика нет скорости, значит отсутствует и центростремительное (нормальное) ускорение \(a_ц\). Тогда применив второй закон Ньютона в проекции на ось \(x\), найдем тангенциальную составляющую ускорения (или просто ускорение \(a_1\)):
\[mg \cdot \sin \alpha = m{a_1}\]
\[{a_1} = g \cdot \sin \alpha \]
Для нижнего положения шарика введем оси как показано на правой части схемы. Вдоль оси \(x\) силы не действуют, значит нет тангенциального ускорения. Раз так, значит ускорение шарика \(a_2\) равно центростремительному (нормальному) ускорению в этой точке. Запишем второй закон Ньютона в проекции на ось \(y\):
\[T – mg = m{a_2}\;\;\;\;(1)\]
\[{a_2} = \frac{T}{m} – g\]
По условию \(a_1=a_2\), поэтому:
\[g \cdot \sin \alpha = \frac{T}{m} – g\]
\[g\left( {1 + \sin \alpha } \right) = \frac{T}{m}\]
\[m = \frac{T}{{g\left( {1 + \sin \alpha } \right)}}\]
Задача решена в общем виде.
Ответ: \(m = \frac{T}{{g\left( {1 + \sin \alpha } \right)}}\).
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.7.56 Тело брошено вертикально вверх со скоростью 30 м/с. Если принять потенциальную
2.8.1 Камень массой 1 кг бросили вертикально вверх с начальной скоростью 2 м/с
2.8.2 Найти скорость винтовки при отдаче, если её масса в 500 раз больше массы пули
Подскажите пожалуйста, что это за единица и откуда она взялась?? g×sin a=T/m-g
g(1+sin a)= T/m
Если применить закон сохранения энергии, получим: m=T/(1,8g).
Угол лишний.
Категорически с Вами не согласен. Как Вы запишете закон сохранения энергии (ЗСЭ) без угла? Да и зачем вам ЗСЭ, если задача решается через второй закон Ньютона для крайних положений шарика.
(ускорения в крайнем и нижнем положениях равны по модулю друг другу)-как это может быть ?
Почему не может? Я вот даже ответ к этой задаче получил.
Вы считаете, что ускорение шарика в верхнем и нижнем положениях равно g?
да, равно g
Нет, чтобы определить ускорение тела, нужно записать второй закон Ньютона.
Ускорение тела будет равно g, если оно падает свободно (только под действием силы тяжести mg), так как по второму закону Ньютона:
mg=ma, a=g
Тут же шарик движется несвободно, на него также действует сила натяжения нити T (так называемая связь), причем направление действия этой силы по мере движения меняется.
Вот чтобы определить ускорение шарика в любой точке его траектории, нужно изобразить все силы, действующие на него в этой точке, найти их проекции на удобные оси, и таким образом найти ускорение через второй закон Ньютона. Собственно этим в этой задаче мы и занимались, правда мы искали массу, а не ускорения.
Спасибо