Условие задачи:

Шарик массой \(m\), подвешенный на нити, отклонен от положения равновесия на угол 90° и отпущен. Какова должна быть прочность нити, чтобы шарик при движении не оборвал её?

Задача №2.8.33 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(m\), \(\alpha=90^\circ\), \(T_{max}-?\)

Решение задачи:

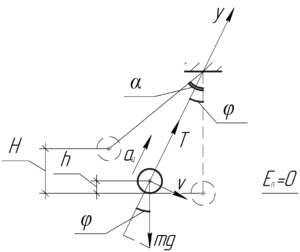Перефразируя вопрос задачи, нам нужно найти максимальную силу натяжения нити в процессе движения шарика. Если мы возьмем нить, которая способна выдержать эту максимальную силу натяжения, то тогда нить никогда не оборвётся.

Но мы не знаем в какой точке траектории движения шарика сила натяжения будет принимать наибольшее значение. Чтобы определить её (точку), выберем произвольное положение шарика в процессе движения, когда он будет иметь скорость \(\upsilon\), а нить будет составлять с вертикалью угол \(\varphi\).

Запишем второй закон Ньютона в проекции на ось \(y\), которая совпадает с нитью (смотрите схему):

\[T — mg \cdot \cos \varphi  = m{a_ц}\;\;\;\;(1)\]

Центростремительное ускорение шарика найдем по следующей формуле, где \(l\) — длина нити:

\[{a_ц} = \frac{{{\upsilon ^2}}}{l}\]

Подставив эту формулу в выражение (1) и выразив натяжение нити \(T\), получим:

\[T = m\left( {g \cdot \cos \varphi  + \frac{{{\upsilon ^2}}}{l}} \right)\]

Найдем скорость шарика в этом положении через закон сохранения энергии. Выберем нуль потенциальной энергии в самой нижней точке траектории шарика, тогда:

\[mgH = \frac{{m{\upsilon ^2}}}{2} + mgh\]

\[mgl\left( {1 — \cos \alpha } \right) = \frac{{m{\upsilon ^2}}}{2} + mgl\left( {1 — \cos \varphi } \right)\]

Так как по условию \(\alpha=90^\circ\), то \(\cos \alpha  = 0\). Выразим квадрат скорости из последнего выражения:

\[mgl = \frac{{m{\upsilon ^2}}}{2} + mgl — mgl\cos \varphi \]

\[{\upsilon ^2} = 2gl\cos \varphi \]

Подставим полученное в формулу (1), тогда:

\[T = m\left( {g \cdot \cos \varphi  + \frac{{2gl\cos \varphi }}{l}} \right)\]

\[T = 3mg\cos \varphi \]

Видно, что сила натяжения нити зависит от текущего угла между нитью и вертикалью. Так как косинус — функция убывающая, то сила натяжения нити примет свой максимум, когда угол \(\varphi\) станет равен нулю, т.е. \(\cos \varphi  = 1\). Значит:

\[{T_{max}} = 3mg\]

Если Вы хотите закрепить свои знания в решении подобных задач, то можете посмотреть аналогичную задачу.

Ответ: \(3mg\).

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

2.8.32 С какой начальной скоростью v0 нужно бросить вниз мяч с высоты h, чтобы он
2.8.34 Шарик подбросили вверх, сообщив ему кинетическую энергию 20 Дж. Через
2.8.35 Мяч падает с высоты 7,5 м на гладкий пол. Какую скорость нужно сообщить мячу