Условие задачи:

С ледяной горки высотой 3 м и длиной основания 5 м съезжают санки, которые останавливаются, пройдя путь по горизонтали 95 м. Найти коэффициент трения, считая его везде постоянным.

Задача №2.3.10 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

$H=3$ м, $L=5$ м, $S=95$ м, $\mu-?$

Решение задачи:

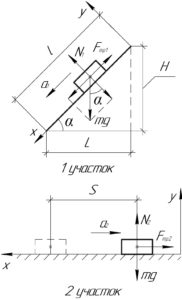На схеме покажем два участка движения санок (условно) с системой координат: по горке и по горизонтальной поверхности. Понятно, что на обоих участках сила трения скольжения принимает разные значения.

1 участок: движение по горки. Тело покоится по оси $y$, из первого закона Ньютона в проекции на эту ось следует, что:

$$N_1 = mg \cdot \cos \alpha$$

Сила трения скольжения определяется по формуле:

$${F_{тр1}} = \mu N_1$$

$${F_{тр1}} = \mu mg \cdot \cos \alpha \;\;\;\;(1)$$

При этом на этом участке сила трения совершит такую работу (она, кстати, отрицательна):

$${A_1} =  — {F_{тр}} \cdot l$$

Подставим выражение (1) в последнюю формулу, тогда:

$${A_1} =  — \mu mg \cdot \cos \alpha  \cdot l$$

Обратите внимание, что из геометрии произведение $l \cdot \cos \alpha$ равно $L$. Тогда:

$${A_1} =  — \mu mg \cdot L\;\;\;\;(2)$$

2 участок: движение по горизонтальной поверхности. Аналогично, по первому закону Ньютона в проекции на ось $y$:

$$N_2 = mg$$

Сила трения скольжения уже равна:

$${F_{тр2}} = \mu mg\;\;\;\;(3)$$

Работу силы трения скольжения $F_{тр2}$ найдем по формуле:

$${A_2} =  — {F_{тр2}} \cdot S$$

Учитывая (3), имеем:

$${A_2} =  — \mu mg \cdot S\;\;\;\;(4)$$

По закону сохранения энергии работа неконсервативных сил есть изменение полной механической энергии. На вершине горки тело имело потенциальную энергию, а, спустившись по горке и пройдя расстояние $S$, ни потенциальной, ни кинетической.

$$A = \Delta E$$

$${A_1} + {A_2} = 0 — mgH$$

Учитывая ранее полученные выражения для работ (2) и (4), имеем:

$$— \mu mg \cdot L — \mu mg \cdot S =  — mgH$$

$$\mu  = \frac{H}{{L + S}}$$

Посчитаем численный ответ:

$$\mu  = \frac{3}{{5 + 95}} = 0,03$$

Задачу можно решить иначе (я бы не сказал, что проще), используя второй закон Ньютона, формулы кинематики и тригонометрию. Сначала запишем второй закон Ньютона в проекции на ось $x$ для двух участков (как мы определяли силы трения скольжения и силу реакции опоры на этих участках, читайте выше):

$$\left\{ \begin{gathered} mg \cdot \sin \alpha — \mu mg \cdot \cos \alpha = m{a_1} \hfill \\ \mu mg = m{a_2} \hfill \\ \end{gathered} \right.$$

$$\left\{ \begin{gathered} {a_1} = g\left( {\sin \alpha — \mu \cdot \cos \alpha } \right) \hfill \\ {a_2} = \mu g \hfill \\ \end{gathered} \right.$$

Учитывая, что скорость санок в начале и в конце равна нулю, а на участке перехода от первого участка ко второму — равна некой $\upsilon$, примем формулу кинематики без времени (опять же для двух участков):

$$\left\{ \begin{gathered} {\upsilon ^2} — {0^2} = 2{a_1}l \hfill \\ {0^2} — {\upsilon ^2} = — 2{a_2}S \hfill \\ \end{gathered} \right.$$

$$\left\{ \begin{gathered} {\upsilon ^2} = 2{a_1}l \hfill \\ {\upsilon ^2} = 2{a_2}S \hfill \\ \end{gathered} \right.$$

Замечательно, значит справедливо равенство:

$$2{a_1}l = 2{a_2}S$$

$${a_1}l = {a_2}S$$

Подставим полученные выражения для ускорений, тогда:

$$g\left( {\sin \alpha — \mu \cdot \cos \alpha } \right)l = \mu gS$$

$$\left( {\sin \alpha — \mu \cdot \cos \alpha } \right)l = \mu S$$

Из рисунка 1-го участка видно, что:

$$\left\{ \begin{gathered} \sin \alpha = \frac{H}{l} \hfill \\ \cos \alpha = \frac{L}{l} \hfill \\ \end{gathered} \right.$$

Тогда:

$$\left( {\frac{H}{l} — \mu \cdot \frac{L}{l}} \right)l = \mu S$$

$$H — \mu L = \mu S$$

$$H = \mu \left( {L + S} \right)$$

Откуда мы получим то же самое решение, что и в первом случае:

$$\mu = \frac{H}{{L + S}}$$

$$\mu  = \frac{3}{{5 + 95}} = 0,03$$

Ответ: 0,03.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

2.3.9 Автомобиль при полностью включенных тормозах (колеса не вращаются) может
2.3.11 Брусок массой 3 кг находится на наклонной плоскости, составляющей угол 45 градусов
2.3.12 Брусок сползает без начальной скорости с высоты 2 м по доске, наклоненной