Условие задачи:

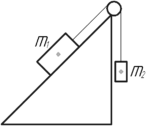С каким ускорением движутся грузы $m_1=0,5$ кг и $m_2=0,6$ кг, если высота наклонной плоскости $H=60$ см, длина наклонной плоскости $l=1$ м и коэффициент трения первого груза о плоскость 0,25? Невесомый блок вращается по часовой стрелке.

Задача №2.3.15 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

$m_1=0,5$ кг, $m_2=0,6$ кг, $H=60$ см, $l=1$ м, $\mu=0,25$, $a-?$

Решение задачи:

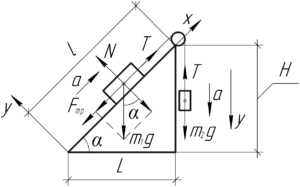Сделав схему к задаче, введем координатные оси для каждого груза и покажем все силы, действующие на них (смотрите схему). Грузы движутся ускоренно, причем первый груз поднимается по плоскости, а второй — опускается вниз, так как блок вращается по часовой стрелке. Запишем второй закон Ньютона для второго груза в проекции на ось $y$:

$${m_2}g — T = {m_2}a\;\;\;\;(1)$$

Для первого груза запишем второй закон Ньютона в проекции на ось $x$ и первый закон Ньютона в проекции на ось $y$:

$$\left\{ \begin{gathered} T — {m_1}g\sin \alpha — {F_{тр}} = {m_1}a \;\;\;\;(2)\hfill \\ N = {m_1}g\cos \alpha \;\;\;\;(3)\hfill \\ \end{gathered} \right.$$

Силу трения скольжения определяют по следующей формуле:

$${F_{тр}} = \mu N$$

Так как мы уже определили силу реакции опоры (формула (3)), то:

$${F_{тр}} = \mu {m_1}g\cos \alpha$$

Полученное подставим в (2), тогда:

$$T — {m_1}g\sin \alpha  — \mu {m_1}g\cos \alpha  = {m_1}a\;\;\;\;(4)$$

Теперь сложим равенства (1) и (4), в итоге получим:

$${m_2}g — {m_1}g\sin \alpha  — \mu {m_1}g\cos \alpha  = \left( {{m_1} + {m_2}} \right)a\;\;\;\;(5)$$

Вы должны заметить, что нам неизвестен угол наклонной плоскости $\alpha$ и тригонометрические функции этого угла. Но их можно выразить через геометрические параметры наклонной плоскости, что мы сейчас и сделаем. Для начала определим длину основания наклонной плоскости по теореме Пифагора:

$$L = \sqrt {{l^2} — {H^2}}$$

Тогда синус и косинус угла $\alpha$ по определению равны:

$$\sin \alpha  = \frac{H}{l}$$

$$\cos \alpha  = \frac{L}{l} = \frac{{\sqrt {{l^2} — {H^2}} }}{l}$$

Полученное подставим в (5), далее домножим обе части равенства на $l$ и выразим искомое ускорение $a$:

$${m_2}g — {m_1}g\frac{H}{l} — \mu {m_1}g\frac{{\sqrt {{l^2} — {H^2}} }}{l} = \left( {{m_1} + {m_2}} \right)a$$

$${m_2}gl — {m_1}gH — \mu {m_1}g\sqrt {{l^2} — {H^2}}  = \left( {{m_1} + {m_2}} \right)al$$

$$a = \frac{{g\left( {{m_2}l — {m_1}H — \mu {m_1}\sqrt {{l^2} — {H^2}} } \right)}}{{\left( {{m_1} + {m_2}} \right)l}}$$

Переведем высоту $H$ в систему СИ:

$$60\; см = \frac{{60}}{{100}}\; м = 0,6\; м$$

Посчитаем численный ответ:

$$a = \frac{{10 \cdot \left( {0,6 \cdot 1 — 0,5 \cdot 0,6 — 0,25 \cdot 0,5 \cdot \sqrt {{1^2} — {{0,6}^2}} } \right)}}{{\left( {0,5 + 0,6} \right) \cdot 1}} = 1,82\; м/с^2$$

Ответ: 1,82 м/с².

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

2.3.14 Ледяная горка составляет с горизонтом угол 10 градусов. По ней пускают вверх камень
2.3.16 С горы высотой 2 м и основанием 5 м съезжают санки, которые затем останавливаются
2.3.17 Чему должен быть равен минимальный коэффициент трения между шинами