Условие задачи:
Радиус Земли равен 6400 км. На каком расстоянии от поверхности Земли сила притяжения космического корабля к ней станет в 9 раз меньше, чем на поверхности Земли?
Задача №2.5.22 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(R=6400\) км, \(F_{т2}=\frac{F_{т1}}{9}\), \(h-?\)
Решение задачи:
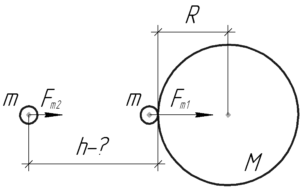Сила притяжения космического корабля к Земле определяется законом всемирного тяготения. При этом силу притяжения на поверхности Земли и на некоторой высоте \(h\) можно соответственно найти по формулам:
\[\left\{ \begin{gathered}
{F_{т1}} = G\frac{{Mm}}{{{R^2}}} \hfill \\
{F_{т2}} = G\frac{{Mm}}{{{{\left( {R + h} \right)}^2}}} \hfill \\
\end{gathered} \right.\]
Поделим верхнюю формулу на нижнюю. Так как в задаче сказано, что \(F_{т2}=\frac{F_{т1}}{9}\), то:
\[\frac{{{{\left( {R + h} \right)}^2}}}{{{R^2}}} = 9\]
\[\frac{{R + h}}{R} = 3\]
\[R + h = 3R\]
\[h = 2R\]
Численно эта высота равна (переводить в СИ не будем):
\[h = 2 \cdot 6400 = 12800\; км\]
Ответ: 12800 км.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.5.21 На каком расстоянии от центра Земли (в долях радиуса Земли R) ускорение свободного
2.6.1 Для сжатия пружины на 2 см надо приложить силу 10 Н. Определить энергию упругой
2.6.2 Какую работу надо совершить, чтобы удлинить на 0,1 м резиновый шнур с коэффициентом