Условие задачи:

Пуля массой 10 г, летевшая со скоростью 400 м/с, пробив доску толщиной 5 см, уменьшила скорость вдвое. Определить среднюю силу сопротивления доски движению пули.

Задача №2.1.27 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(m=10\) г, \(\upsilon_0=400\) м/с, \(S=5\) см, \(\upsilon=\frac{\upsilon_0}{2}\), \(F-?\)

Решение задачи:

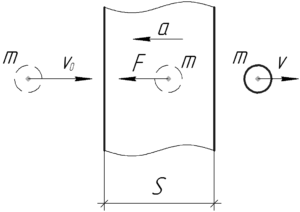Задачу можно решить двумя способами, первый способ более сложный, чем второй, тем не менее они оба укладываются в рамки обычного курса физики.

Первый способ — основан на применении второго закона Ньютона в, так называемом, общем виде.

\[F = \frac{{\Delta p}}{{\Delta t}}\;\;\;\;(1)\]

То есть сила сопротивления со стороны доски \(F\) равна отношению изменения импульса пули \(\Delta p\) ко времени движения пули в доске \(\Delta t\).

Импульс пули равен произведению массы пули на её скорость, тогда изменение импульса пули найти проще простого.

\[\Delta p = m\upsilon  — m{\upsilon _0} = m\left( {\upsilon  — {\upsilon _0}} \right)\]

Так как по условию скорость пули снизиться в 2 раза, то есть \(\upsilon=\frac{\upsilon_0}{2}\), то:

\[\Delta p = m\left( {\frac{{{\upsilon _0}}}{2} — {\upsilon _0}} \right) =  — \frac{{m{\upsilon _0}}}{2}\]

Знак «минус» показывает направление действия силы, при подстановке в выражение второго закона Ньютона (самая первая формула) его можно отбрасывать.

Осталось найти время движения пули в доске. Если на пулю действовала какая-то не изменяющаяся во времени (средняя) сила сопротивления \(F\), то она создала постоянное во времени ускорение \(a\). Воспользуемся известной формулой кинематики без времени:

\[{\upsilon ^2} — \upsilon _0^2 =  — 2aS\]

\[\frac{{\upsilon _0^2}}{4} — \upsilon _0^2 =  — 2aS \Rightarrow \frac{{3\upsilon _0^2}}{4} = 2aS \Rightarrow a = \frac{{3\upsilon _0^2}}{{8S}}\]

Формула скорости для равнозамедленного движения применительно к этой задаче:

\[\upsilon {\text{ }} = {\upsilon _0} — a\Delta t\]

Так как по условию \(\upsilon=\frac{\upsilon_0}{2}\), то:

\[\frac{{{\upsilon _0}}}{2} = {\upsilon _0} — a\Delta t \Rightarrow \Delta t = \frac{{{\upsilon _0}}}{{2a}}\]

Подставим в последнюю формулу полученное нами выражение для ускорения \(a\).

\[\Delta t = \frac{{{\upsilon _0} \cdot 8S}}{{2 \cdot 3\upsilon _0^2}} = \frac{{4S}}{{3{\upsilon _0}}}\]

В конце концов подставим выражения для изменения импульса и времени в формулу (1).

\[F = \frac{{m{\upsilon _0} \cdot 3{\upsilon _0}}}{{2 \cdot 4S}} = \frac{{3m\upsilon _0^2}}{{8S}}\]

Посчитаем численный ответ, подставив данные задачи (переведя их в систему СИ) в формулу.

\[F = \frac{{3 \cdot 0,01 \cdot {{400}^2}}}{{8 \cdot 0,05}} = 12000\; Н = 12\; кН\]

Второй способ — для решения задачи применим закон сохранения энергии (или теорему об изменении кинетической энергии, как хотите). До попадания в доску у пули была одна кинетическая энергия, после вылета из доски — другая, но меньшая, вследствие того, что сила сопротивления совершила работу.

Напомним, что кинетическую энергию можно найти как половину произведения массы тела на квадрат скорости, работу силы — как скалярное произведение вектора силы на вектор перемещения.

\[ — FS = \frac{{m{\upsilon ^2}}}{2} — \frac{{m\upsilon _0^2}}{2}\]

\[\frac{{m\upsilon _0^2}}{2} = FS + \frac{{m{\upsilon ^2}}}{2}\]

Не забывайте, что работа силы сопротивления отрицательна, так как вектор силы и вектор перемещения противонаправлены. Так как \(\upsilon=\frac{\upsilon_0}{2}\), то:

\[\frac{{m\upsilon _0^2}}{2} = FS + \frac{{m\upsilon _0^2}}{8} \Rightarrow F = \frac{{3m\upsilon _0^2}}{{8S}}\]

Как видите, мы получили тот же ответ, но гораздо быстрее. Тем не менее оба способа интересны и достойны запоминания.

Ответ: 12 кН.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

2.1.26 Два автомобиля массами m и 2m движутся в одном направлении с одинаковыми
2.1.28 Пуля массой 9 г, летевшая со скоростью 600 м/с, попадает в деревянную стену
2.1.29 На тело, движущееся по горизонтальной поверхности, действуют следующие силы