Решение: При вращении шарика, прикрепленного к пружине длиной 20 см, с частотой вращения

Условие задачи:

При вращении шарика, прикрепленного к пружине длиной 20 см, с частотой вращения 10 об/с, пружина удлинилась на 2 см. При какой частоте вращения удлинение пружины будет равно 3 см?

Задача №2.6.5 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(l=20\) см, \(\nu_1=10\) об/с, \(x_1=2\) см, \(x_2=3\) см, \(\nu_2-?\)

Решение задачи:

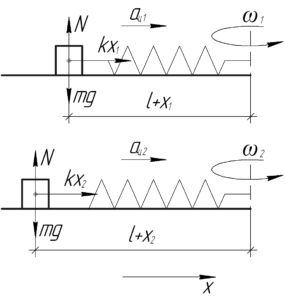При вращении шарика по горизонтальной поверхности сила упругости сообщает ему центростремительное ускорение, поэтому второй закон Ньютона в проекции на ось \(x\) запишется в следующем виде:

\[k{x_1} = m{a_{ц1}}\;\;\;\;(1)\]

Так как в первом случае шарик в процессе вращения находится на расстоянии \(\left( {l + {x_1}} \right)\) от оси вращения, то центростремительное ускорение \(a_{ц1}\) найдем по такой формуле, где \(\omega\) – это угловая скорость вращения.

\[{a_{ц1}} = \omega _1^2\left( {l + {x_1}} \right)\]

Формула связи угловой скорости с частотой вращения выглядит так:

\[{\omega _1} = 2\pi {\nu _1}\]

Поэтому:

\[{a_{ц1}} = 4{\pi ^2}\nu _1^2\left( {l + {x_1}} \right)\]

Равенство (1) примет такой вид:

\[k{x_1} = 4{\pi ^2}\nu _1^2\left( {l + {x_1}} \right)m\;\;\;\;(2)\]

Аналогично для второго случая:

\[k{x_2} = 4{\pi ^2}\nu _2^2\left( {l + {x_2}} \right)m\;\;\;\;(3)\]

Поделим равенства (3) и (2) друг на друга, получим:

\[\frac{{{x_2}}}{{{x_1}}} = \frac{{\nu _2^2\left( {l + {x_2}} \right)}}{{\nu _1^2\left( {l + {x_1}} \right)}}\]

\[{\nu _2} = {\nu _1}\sqrt {\frac{{{x_2}\left( {l + {x_1}} \right)}}{{{x_1}\left( {l + {x_2}} \right)}}} \]

Мы получили решение задачи в общем виде. Переведем некоторые данные в систему СИ (именно в этой задаче этого можно и не делать) и произведем расчет численного ответа.

\[20\; см = \frac{20}{{100}}\; м = 0,2\; м\]

\[2\; см = \frac{2}{{100}}\; м = 0,02\; м\]

\[3\; см = \frac{3}{{100}}\; м = 0,03\; м\]

\[{\nu _2} = 10\sqrt {\frac{{0,03 \cdot \left( {0,2 + 0,02} \right)}}{{0,02 \cdot \left( {0,2 + 0,03} \right)}}} = 11,98\; Гц \approx 12\; Гц\]