Условие задачи:

Поезд движется по закруглению со скоростью 50 км/ч. Шарик, подвешенный в вагоне, отклоняется на угол 5°. Определить радиус закругления.

Задача №2.4.25 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(\upsilon=50\) км/ч, \(\alpha=5^\circ\), \(R-?\)

Решение задачи:

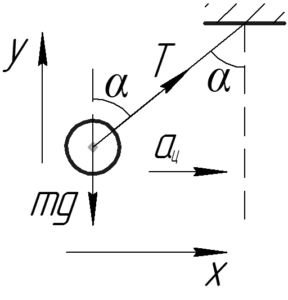Рассмотрим шарик в инерциальной системе отсчета, связанной с Землей. Запишем первый закон Ньютона в проекции на ось \(y\), так как вдоль этого направления шарик покоится:

\[T \cdot \cos \alpha  = mg\;\;\;\;(1)\]

Так как поезд движется по закруглению некого радиуса \(R\), значит на шарик действует центростремительное ускорение \(a_ц\), зависящее от скорости шарика (поезда) \(\upsilon\) и радиуса \(R\) по такой формуле:

\[{a_ц} = \frac{{{\upsilon ^2}}}{R}\]

Второй закон Ньютона в проекции на ось \(x\):

\[T \cdot \sin \alpha  = m{a_ц}\]

\[T \cdot \sin \alpha  = m\frac{{{\upsilon ^2}}}{R}\;\;\;\;(2)\]

Разделим равенства (2) и (1) друг на друга, получим:

\[tg\alpha  = \frac{{{\upsilon ^2}}}{{gR}}\]

\[R = \frac{{{\upsilon ^2}}}{{g \cdot tg\alpha }}\]

Задача решена, осталось посчитать численный ответ, предварительно переведя скорость поезда в систему СИ.

\[50\; км/ч = \frac{{50 \cdot 1000}}{{1 \cdot 3600}}\; м/с = \frac{{125}}{9}\; м/с\]

\[R = \frac{{{{125}^2}}}{{{9^2} \cdot 10 \cdot tg5^\circ }} = 220,5\; м\]

Кстати, шарик можно было рассмотреть и в системе отсчета (СО), связанной с поездом. Правда эта СО неинерциальная, но эту неинерциальность можно было компенсировать, приложив к шарику центробежную силу.

Ответ: 220,5 м.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

2.4.24 По гладкому столу вращается груз, прикрепленный к центру вращения пружиной
2.4.26 Подвешенный на нити шарик массой 0,3 кг совершает колебания в вертикальной
2.4.27 Шарик массой 200 г на нити длиной 3 м описывает в горизонтальной плоскости