Условие задачи:
Подвешенному на нити длиной 1 м шарику сообщили начальную скорость такую, что когда нить отклонилась на угол 60° от вертикали, ускорение шарика оказалось направленным горизонтально. Найдите начальную скорость.
Задача №2.8.51 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(L=1\) м, \(\alpha=60^\circ\), \(\upsilon_0-?\)
Решение задачи:
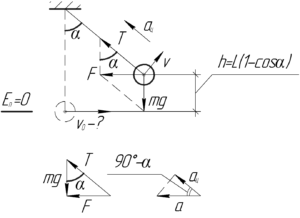 Если ускорение шарика направленно горизонтально, то и равнодействующая всех сил направлена горизонтально. Из второго закона Ньютона она равна:
Если ускорение шарика направленно горизонтально, то и равнодействующая всех сил направлена горизонтально. Из второго закона Ньютона она равна:
\[F = ma\]
На шарик действуют две силы: сила тяжести и сила натяжения нити. Так как сила тяжести направлена вертикально, а равнодействующая горизонтально, то полученный векторный треугольник — прямоугольный. Очевидно, что:
\[tg\alpha = \frac{F}{{mg}}\]
\[tg\alpha = \frac{{ma}}{{mg}} = \frac{a}{g}\]
\[a = g \cdot tg\alpha \;\;\;\;(1)\]
Если ускорение спроецировать на ось, совпадающей с нитью, то мы найдем центростремительное ускорение:
\[{a_ц} = a \cdot \cos \left( {90^\circ — \alpha } \right)\]
Учитывая (1), имеем:
\[{a_ц} = g \cdot tg\alpha \cdot \cos \left( {90^\circ — \alpha } \right)\]
\[{a_ц} = g \cdot tg60^\circ \cdot \cos \left( {90^\circ — 60^\circ } \right) = g \cdot \sqrt 3 \cdot \frac{{\sqrt 3 }}{2}\]
\[{a_ц} = \frac{{3g}}{2}\;\;\;\;(2)\]
С другой стороны, центростремительное ускорение всегда можно найти как отношение квадрата скорости шарика в этой точке к радиусу кривизны траектории (в данном случае равном длине нити \(L\)):
\[{a_ц} = \frac{{{\upsilon ^2}}}{L}\]
Благодаря ранее найденному равенству (2), получим:
\[\frac{{{\upsilon ^2}}}{L} = \frac{{3g}}{2}\]
\[{\upsilon ^2} = \frac{{3gL}}{2}\;\;\;\;(3)\]
Отлично, мы знаем квадрат скорости шарика, когда он отклонился на угол \(\alpha\) — это намёк на применение закона сохранения энергии. Если выбрать уровень нуля потенциальной энергии на уровне начального положения шарика, то в начале у шарика есть только кинетическая энергия \(\frac{{m\upsilon _0^2}}{2}\). Когда же он отклонится на угол \(\alpha\), то у него будет потенциальная энергия \(mgL\left( {1 — \cos \alpha } \right)\) и кинетическая энергия \(\frac{{m{\upsilon ^2}}}{2}\).
\[\frac{{m\upsilon _0^2}}{2} = mgL\left( {1 — \cos \alpha } \right) + \frac{{m{\upsilon ^2}}}{2}\]
Во-первых, домножим на 2 и сократим на \(m\), далее подставим выражение (3):
\[\upsilon _0^2 = 2gL\left( {1 — \cos \alpha } \right) + \frac{{3gL}}{2}\]
В конечном счете, начальная скорость шарика равна:
\[{\upsilon _0} = \sqrt {gL\left( {\frac{7}{2} — 2\cos \alpha } \right)} \]
Подставим данные задачи в последнюю формулу и посчитаем ответ.
\[{\upsilon _0} = \sqrt {10 \cdot 1\left( {\frac{7}{2} — 2\cos 60^\circ } \right)} = 5\; м/с = 18\; км/ч\]
Ответ: 18 км/ч.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.8.50 Плавательный бассейн площадью 100 м2 заполнен водой до глубины 2 м. Требуется
2.8.52 При ударе шарика об идеально гладкую горизонтальную поверхность теряется третья
2.8.53 Шарик на нити отклонили от вертикали на 60 градусов и отпустили без начальной
Спасибо за решение! Возник вопрос — почему мы сразу не можем заменить cos(90∘–α)
на sin(α)?
Как получили \({a_ц} = a \cdot \cos \left( {90^\circ — \alpha } \right)\), после этого можно перейти к синусу, то есть \({a_ц} = a\sin \alpha \) и так далее