Решение: По гладкому столу вращается груз, прикрепленный к центру вращения пружиной

Условие задачи:

По гладкому столу вращается груз, прикрепленный к центру вращения пружиной, частота вращения 2 об/с; пружина растянута вдвое. Определить радиус окружности, если известно, что тот же груз, подвешенный на пружине, деформирует её на 10%.

Задача №2.4.24 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(\nu=2\) об/с, \(x_1=l\), \(x_2=0,1l\), \(R-?\)

Решение задачи:

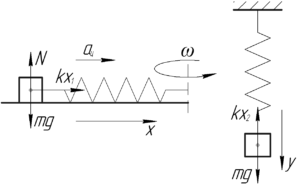Сначала запишем первый закон Ньютона в проекции на ось \(y\) для случая, когда груз подвешен на пружине:

\[mg = kx_2\]

Выразим коэффициент жесткости пружины \(k\):

\[k = \frac{mg}{x_2}\;\;\;\;(1)\]

Теперь применим второй закон Ньютона (в проекции на \(x\)) для случая, когда этот же груз вращается по столу:

\[k{x_1} = m{a_ц}\;\;\;\;(2)\]

Вспомним формулу определения центростремительного ускорения \(a_ц\) через угловую скорость \(\omega\) и формулу связи последней с частотой вращения \(\nu\):

\[{a_ц} = {\omega ^2}R\]

\[\omega = 2\pi \nu \]

Тогда:

\[{a_ц} = 4{\pi ^2}{\nu ^2}R\]

Подставим это выражение в (2):

\[kx_1 = 4{\pi ^2}{\nu ^2}mR\]

В полученное равенство подставим (1), тогда:

\[\frac{mg}{x_2} \cdot {x_1} = 4{\pi ^2}{\nu ^2}mR\]

По условию задачи \(x_1=l\) (если пружина растянута вдвое, значит деформация равна начальной длине пружины) и \(x_2=0,1l\), поэтому:

\[\frac{mg}{0,1l} \cdot l = 4{\pi ^2}{\nu ^2}mR\]

\[10g = 4{\pi ^2}{\nu ^2}R\]

\[R = \frac{5g}{2{\pi ^2}{\nu ^2}}\]