Условие задачи:
Плавательный бассейн площадью 100 м2 заполнен водой до глубины 2 м. Требуется перекачать эту воду на высоту 3 м (считая от поверхности воды в бассейне). Определить работу, которую нужно совершить при этом.
Задача №2.8.50 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(S=100\) м2, \(h=2\) м, \(H=3\) м, \(A-?\)
Решение задачи:
 Насос совершит минимальную работу тогда, когда будет перекачивать жидкость максимально медленно, то есть сообщая жидкости маленькую скорость. В этом случае работа насоса будет равна изменению потенциальной энергии воды.
Насос совершит минимальную работу тогда, когда будет перекачивать жидкость максимально медленно, то есть сообщая жидкости маленькую скорость. В этом случае работа насоса будет равна изменению потенциальной энергии воды.
\[A = \Delta {E_п}\]
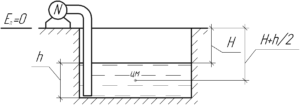
Центр масс всей воды находится на расстоянии \(H+\frac{h}{2}\) от того места, куда нужно перекачать воду (смотрите рисунок). Тогда изменение потенциальной энергии воды равно:
\[\Delta {E_п} = mg\left( {H + \frac{h}{2}} \right)\]
Массу воды в бассейне найдем как произведение плотности воды на её объем, объем же равен произведению площади основания на высоту всей воды.
\[m = \rho V = \rho Sh\]
Окончательно, решение задачи в общем виде такое:
\[A = \rho Shg\left( {H + \frac{h}{2}} \right)\]
Считаем ответ на калькуляторе:
\[A = 1000 \cdot 100 \cdot 2 \cdot 10\left( {3 + \frac{2}{2}} \right) = 8 \cdot {10^6}\; Дж = 8000\; кДж\]
Ответ: 8000 кДж.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.8.49 Небольшое тело соскальзывает по наклонной плоскости, переходящей в мертвую
2.8.51 Подвешенному на нити длиной 1 м шарику сообщили начальную скорость такую
2.8.52 При ударе шарика об идеально гладкую горизонтальную поверхность теряется третья