Условие задачи:

Определить, с каким ускорением падают тела на поверхность Луны, зная, что радиус Луны в 3,8 раза меньше радиуса Земли, а её масса в 81 раз меньше массы Земли (\(g=9,8\) м/с²).

Задача №2.5.12 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(R_л=\frac{R_з}{3,8}\), \(M_л=\frac{M_з}{81}\), \(g_з=9,8\) м/с², \(g_л-?\)

Решение задачи:

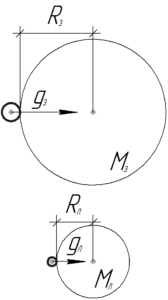Ускорение свободного падения на поверхности Земли \(g_з\) можно определить по формуле:

\[{g_з} = G\frac{{{M_з}}}{{R_з^2}}\;\;\;\;(1)\]

Аналогично, ускорение свободного падения на Луне \(g_л\) равно:

\[{g_л} = G\frac{{{M_л}}}{{R_л^2}}\]

По условию \(R_л=\frac{R_з}{3,8}\) и \(M_л=\frac{M_з}{81}\), поэтому:

\[{g_л} = G\frac{{{{3,8}^2} \cdot {M_з}}}{{81 \cdot R_з^2}}\]

\[{g_л} = \frac{{{{3,8}^2}}}{{81}}G\frac{{{M_з}}}{{R_з^2}}\]

Учитывая (1), имеем:

\[{g_л} = \frac{{{{3,8}^2}}}{{81}}{g_з}\]

Посчитаем ответ:

\[{g_л} = \frac{{{{3,8}^2}}}{{81}} \cdot 9,8 = 1,75\; м/с^2\]

Ответ: 1,75 м/с².

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

2.5.11 Чему равно ускорение свободного падения на высоте, равной половине радиуса
2.5.13 Человек на Земле прыгает на высоту 1 м. На какую высоту, совершив ту же работу, он
2.5.14 Во сколько раз период обращения искусственного спутника, совершающего движение