Условие задачи:
Определить работу, которую нужно произвести для того, чтобы сжать пружину на 10 см, если для сжатия её на 1 см необходима сила 100 Н.
Задача №2.7.15 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(x_1=10\) см, \(x_2=1\) см, \(F_2=100\) Н, \(A-?\)
Решение задачи:
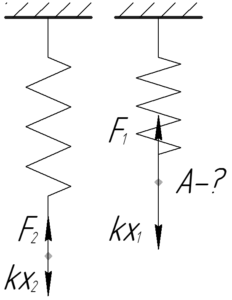Работа \(A\) некоторой внешней силы по сжатию пружины равна изменению потенциальной энергии деформации этой пружины. Так как изначально пружина была недеформирована, то:
\[A = {E_1} = \frac{{kx_1^2}}{2}\;\;\;\;(1)\]
Неизвестную жесткость пружины определим из закона Гука, поскольку известно, что сила \(F_2\) деформирует пружину на величину \(x_2\).
\[{F_2} = k{x_2}\]
\[k = \frac{{{F_2}}}{{{x_2}}}\]
С учётом этого формула (1) преобразуется в следующий вид:
\[A = \frac{{{F_2}x_1^2}}{{2{x_2}}}\]
Так как деформации даны в сантиметрах, то переведем их в систему СИ:
\[10\;см = \frac{{10}}{{100}}\;м = 0,1\;м\]
\[1\;см = \frac{{1}}{{100}}\;м = 0,01\;м\]
Произведем расчет ответа:
\[A = \frac{{100 \cdot {{0,1}^2}}}{{2 \cdot 0,01}} = 50\;Дж\]
Ответ: 50 Дж.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.7.14 На какой высоте над поверхностью Луны тело будет обладать такой же потенциальной
2.7.16 Определить массу тела, имеющего кинетическую энергию 16 Дж, а импульс
2.7.17 Тело массой 1 кг начинает свободно падать. Определить мощность силы тяжести