Определить первую космическую скорость для планеты, масса и радиус которой в два

Условие задачи:

Определить первую космическую скорость для планеты, масса и радиус которой в два раза больше, чем у Земли.

Задача №2.5.7 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(R=2R_3\), \(M=2M_з\), \(\upsilon_1-?\)

Решение задачи:

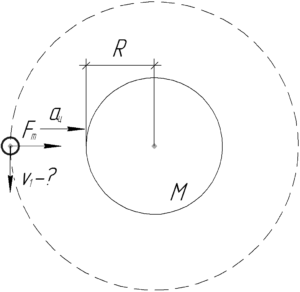Первая космическая скорость – это скорость, которую нужно сообщить телу, чтобы оно стало спутником некоторой планеты. Её можно найти из следующих соображений. При движении спутника по круговой орбите сила тяготения сообщает ему центростремительное ускорение, поэтому второй закон Ньютона даст такое равенство:

\[{F_т} = m{a_ц}\;\;\;\;(1)\]

Силу тяготения найдем из закона всемирного тяготения, учитывая, что высота орбита мала, т.е. она является околоземной:

\[{F_т} = G\frac{{Mm}}{{{R^2}}}\;\;\;\;(2)\]

Центростремительное ускорение спутника, движущегося со скоростью \(\upsilon_1\), равно:

\[{a_ц} = \frac{{\upsilon _1^2}}{R}\;\;\;\;(3)\]

В равенство (1) подставим выражения (2) и (3):

\[G\frac{{Mm}}{{{R^2}}} = \frac{{m\upsilon _1^2}}{R}\]

Значит первую космическую скорость можно определять по такой формуле:

\[{\upsilon _1} = \sqrt {G\frac{M}{R}} \]

По условию \(R=2R_3\) и \(M=2M_з\), поэтому:

\[{\upsilon _1} = \sqrt {G\frac{{2{M_з}}}{{2{R_з}}}}  = \sqrt {G\frac{{{M_з}}}{{{R_з}}}} \]

В принципе после получения этой формулы можно было сказать, что первая космическая скорость на данной планете такая же, как и у Земли. Но мы “добьём” задачу до конца.

Домножим и поделим дробь под корнем на \(R_3\), тогда:

\[{\upsilon _1} = \sqrt {G\frac{{{M_з}}}{{R_з^2}} \cdot {R_з}} \]

Выражение \({G\frac{{{M_з}}}{{R_з^2}}}\) равно ускорению свободного падения \(g\) вблизи поверхности Земли, в итоге имеем:

\[{\upsilon _1} = \sqrt {g{R_з}} \]

Напомним, что радиус Земли равен 6,4·10⁶ м, поэтому численный ответ равен:

\[{\upsilon _1} = \sqrt {10 \cdot 6,4 \cdot {{10}^6}}  = 8000\; м/с\]

Ответ: 8000 м/с.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

2.5.6 На какое расстояние от поверхности Земли нужно удалить тело, чтобы сила тяготения
2.5.8 На некоторой планете сила тяжести, действующая на тело массой 4 кг, равна 8 Н. Найти
2.5.9 На сферической планете вес тела на полюсе в 3 раза больше веса тела на экваторе