Решение: Найти количество теплоты, выделившейся при абсолютно неупругом ударе свинцового

Условие задачи:

Найти количество теплоты, выделившейся при абсолютно неупругом ударе свинцового шара массой 1 кг об очень тяжелую стенку, движущуюся со скоростью 5 см/с. Шар до удара двигался не вращаясь перпендикулярно стенке, навстречу ей со скоростью 10 см/с.

Задача №2.10.26 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

$m=1$ кг, $u=5$ см/с, $\upsilon=10$ см/с, $M \gg m$ , $Q-?$

Решение задачи:

Эту задачу можно решать двумя способами.

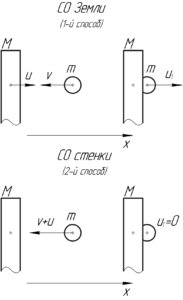
Первый способ. Запишем закон сохранения импульса в проекции на ось $x$ и закон сохранения энергии для системы тел «шар — стенка» в системе отсчета (СО) Земли. Замечу, что этот способ достаточно трудоёмкий, по сравнению со вторым.

$\left\{ \begin{gathered} Mu — m\upsilon = \left( {M + m} \right){u_1} \;\;\;\;(1)\hfill \\ \frac{{M{u^2}}}{2} + \frac{{m{\upsilon ^2}}}{2} = \frac{{\left( {M + m} \right)u_1^2}}{2} + Q \;\;\;\;(2)\hfill \\ \end{gathered} \right.$

Из равенства (1) выразим скорость стенки с шаром $u_1$ после удара:

${u_1} = \frac{{Mu — m\upsilon }}{{M + m}}$

Полученное выражение для скорости $u_1$ подставим в (2).

$\frac{{M{u^2}}}{2} + \frac{{m{\upsilon ^2}}}{2} = \frac{{\left( {M + m} \right)}}{2} \cdot \frac{{{{\left( {Mu — m\upsilon } \right)}^2}}}{{{{\left( {M + m} \right)}^2}}} + Q$

$\frac{{M{u^2}}}{2} + \frac{{m{\upsilon ^2}}}{2} = \frac{{{{\left( {Mu — m\upsilon } \right)}^2}}}{{2\left( {M + m} \right)}} + Q$

Оставим искомое количество теплоты $Q$ в одной стороне, все остальные члены перенесем в другую, где приведем их под общий знаменатель.

$Q = \frac{{M{u^2}}}{2} + \frac{{m{\upsilon ^2}}}{2} — \frac{{{{\left( {Mu — m\upsilon } \right)}^2}}}{{2\left( {M + m} \right)}}$

$Q = \frac{{M{u^2}\left( {M + m} \right) + m{\upsilon ^2}\left( {M + m} \right) — {{\left( {Mu — m\upsilon } \right)}^2}}}{{2\left( {M + m} \right)}}$

Раскроем в числителе скобки и квадрат разности:

$Q = \frac{{{M^2}{u^2} + mM{u^2} + mM{\upsilon ^2} + {m^2}{\upsilon ^2} — {M^2}{u^2} + 2Mmu\upsilon — {m^2}{\upsilon ^2}}}{{2\left( {M + m} \right)}}$

$Q = \frac{{mM{u^2} + mM{\upsilon ^2} + 2Mmu\upsilon }}{{2\left( {M + m} \right)}}$

Вынесем в числителе общий множитель $mM$ за скобки:

$Q = \frac{{mM\left( {{u^2} + 2u\upsilon + {\upsilon ^2}} \right)}}{{2\left( {M + m} \right)}}$

$Q = \frac{{mM{{\left( {u + \upsilon } \right)}^2}}}{{2\left( {M + m} \right)}}$

Воспользуемся основным свойством дроби и поделим и числитель и знаменатель на $M$ .

$Q = \frac{{m{{\left( {u + \upsilon } \right)}^2}}}{{2\left( {1 + \frac{m}{M}} \right)}}$

Так как по условию стенка очень тяжелая, то есть $M \gg m$ , то отношение ${\frac{m}{M}}$ стремится к нулю, значит им можно пренебречь. В итоге конечная формула такая:

$Q = \frac{{m{{\left( {u + \upsilon } \right)}^2}}}{2}$

Второй способ. Перейдем в систему отсчета (СО), связанную с массивной стенкой. В этой СО скорость свинцового шарика равна $\upsilon + u$ и направлена к стенке. После удара скорость шарика станет такой же, как и у стенки, то есть в этой СО станет равной нулю. Получается, что вся кинетическая энергия шарика в этой СО перейдет в теплоту:

$Q = \frac{{m{{\left( {u + \upsilon } \right)}^2}}}{2}$

Как Вы видите, второй способ решения этой задачи существенно короче.

Переведем скорости в систему СИ, а уже потом будет считать ответ:

$5\; см/с = \frac{5}{{100}}\; м/с = 0,05\; м/с$

$10\; см/с = \frac{10}{{100}}\; м/с = 0,10\; м/с$

$Q = \frac{{1{{\left( {0,05 + 0,1} \right)}^2}}}{2} = 0,01125\; Дж = 11,25\; мДж$