Начальная скорость пули 600 м/с, её масса 10 г. Под каким углом к горизонту она

Условие задачи:

Начальная скорость пули 600 м/с, её масса 10 г. Под каким углом к горизонту она вылетела из дула ружья, если её кинетическая энергия в высшей точке траектории равна 450 Дж?

Задача №2.7.42 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(\upsilon_0=600\) м/с, \(m=10\) г, \(E_к=450\) Дж, \(\alpha-?\)

Решение задачи:

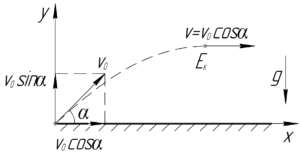В наивысшей точке траектории модуль скорости пули равен:

\[\upsilon  = {\upsilon _0} \cdot \cos \alpha \;\;\;\;(1)\]

Кинетическую энергию пули в этой точке легко найти по следующей формуле:

\[{E_к} = \frac{{m{\upsilon ^2}}}{2}\]

Учитывая выражения (1), формула примет вид:

\[{E_к} = \frac{{m\upsilon _0^2 \cdot {{\cos }^2}\alpha }}{2}\]

Тогда:

\[{\cos ^2}\alpha  = \frac{{2{E_к}}}{{m\upsilon _0^2}}\]

\[\cos \alpha  = \sqrt {\frac{{2{E_к}}}{{m\upsilon _0^2}}} \]

Выразим из формулы искомый угол \(\alpha\):

\[\alpha  = \arccos \left( {\sqrt {\frac{{2{E_к}}}{{m\upsilon _0^2}}} } \right)\]

Переведем массу пули в килограммы (чтобы перевести в систему СИ) и посчитаем ответ:

\[10\;г = \frac{{10}}{{1000}}\;кг = 0,01\;кг\]

\[\alpha  = \arccos \left( {\sqrt {\frac{{2 \cdot 450}}{{0,01 \cdot {{600}^2}}}} } \right) = 60^\circ  = 1,05\;рад\]

Ответ: 1,05 рад.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

2.7.41 На рисунке приведена зависимость потенциальной энергии от времени движения
2.7.43 Самолет массой 2 т летит со скоростью 50 м/с. На высоте 420 м он переходит на снижение
2.7.44 Тело массой 3 кг падает вертикально вниз с начальной скоростью 2 м/с. Найти работу