Условие задачи:
На нити длиной 1 м подвешено тело массой 1 кг. На какой максимальный угол можно его отклонить, чтобы при движении нить не оборвалась? Нить может выдержать нагрузку, превосходящую вес тела в 2 раза.
Задача №2.8.30 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(l=1\) м, \(m=1\) кг, \(T_{max}=2mg\), \(\alpha-?\)
Решение задачи:
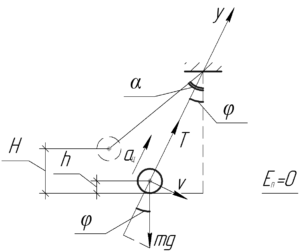Давайте узнаем в какой точке траектории сила натяжения нити примет максимальное значение. Для этого нарисуем произвольное положение тела, при котором оно имеет скорость \(\upsilon\), а угол между нитью и вертикалью составляет \(\varphi\). Для этого положения запишем второй закон Ньютона в проекции на ось, совпадающей с нитью (ось \(y\) на схеме):
\[T — mg\cos \varphi = m{a_ц}\]
Центростремительное ускорение тела можно найти по формуле:
\[a = \frac{{{\upsilon ^2}}}{l}\]
Тогда:
\[T = m\left( {g\cos \varphi + \frac{{{\upsilon ^2}}}{l}} \right)\;\;\;\;(1)\]
Легко понять, что изначально тело находится на высоте \(H = l\left( {1 — \cos \alpha } \right)\). В произвольной выбранной точке тело будет уже находиться на высоте \(h = l\left( {1 — \cos \varphi } \right)\). Из закона сохранения энергии следует:
\[mgH = \frac{{m{\upsilon ^2}}}{2} + mgh\]
\[mgl\left( {1 — \cos \alpha } \right) = \frac{{m{\upsilon ^2}}}{2} + mgl\left( {1 — \cos \varphi } \right)\]
\[{\upsilon ^2} = 2gl\left( {\cos \varphi — \cos \alpha } \right)\;\;\;\;(2)\]
Подставим выражение (2) в (1).
\[T = m\left( {g\cos \varphi + \frac{{2gl\left( {\cos \varphi — \cos \alpha } \right)}}{l}} \right)\]
\[T = mg\left( {3\cos \varphi — 2\cos \alpha } \right)\]
Так как начальный угол отклонения \(\alpha\) и масса тела \(m\) есть величины постоянные, то очевидно, что сила натяжения будет тем больше, чем больше косинус угла \(\varphi\), а он тем больше, чем угол \(\varphi\) меньше (так как косинус — убывающая функция).
Значит максимальное значение силы натяжения будет иметь место при угле \(\varphi\) равно 0° (\(\cos \varphi = 1\)), то есть в нижней точке траектории.
\[{T_{max}} = mg\left( {3 — 2 \cos \alpha } \right)\]
По условию \(T_{max}=2mg\), значит:
\[2mg = mg\left( {3 — 2\cos \alpha } \right)\]
\[3 — 2\cos \alpha = 2\]
\[\cos \alpha = \frac{1}{2} \Rightarrow \alpha = 60^\circ = \frac{\pi }{3}\]
Ответ: \(\frac{\pi}{3}\).
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.8.29 Камень бросили под углом 60 градусов к горизонту со скоростью 15 м/с. Найдите
2.8.31 Пуля, летящая горизонтально со скоростью 400 м/с, попадает в ящик, лежащий
2.8.32 С какой начальной скоростью v0 нужно бросить вниз мяч с высоты h, чтобы он
Объясните пожалуйста,почему H=l(1—cosα)?
Вот в этой задаче объяснено подробно
Да, да, благодарю, Вы правы…
Еще один вопрос. Предположим, начальное положение нити горизонтально, то есть α=pi/2, следовательно cosa=0 и формула принимает вид T=3mgcosφ. В таком случае при вертикальном положении нити, то есть когда тело в самой нижней точке своей траектории, φ=0 и, следовательно, cosφ=1… Получается, что в этом положении T=3mg… Это верно?
Да, все верно.
Даже есть такая задача — решается аналогично, можете почитать https://easyfizika.ru/zadachi/dinamika/sharik-massoj-m-podveshennyj-na-niti-otklonen-ot-polozheniya-ravnovesiya-na-ugol/
Odin vopros. Dopustim a=pi/2, togda 2cosa=2.
V polojenii tela, kogda ugol f=pi/2, to est nit gorizontalna, cosf=0, poluchaetsia T=-2mg. Kak eto poniat?
Spasibo.
Если у вас a=pi/2 (cos a=0), т.е. начальное положение нити — горизонтальное, и вы хотите узнать натяжение нити в этом же положении (f=pi/2, cos f=0), то:
T=mg(3*0-2*0)=0
Короче говоря, Вы неправильно посчитали косинус.