Условие задачи:
На материальную точку массы 1 кг действует две постоянные взаимно перпендикулярные силы. Ускорения, сообщаемые точке каждой силой в отдельности, равны 3 и 4 м/с2. Чему равна величина результирующей силы, действующей на точку?
Задача №2.1.90 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(m=1\) кг, \(a_1=3\) м/с2, \(a_2=4\) м/с2, \(F-?\)
Решение задачи:
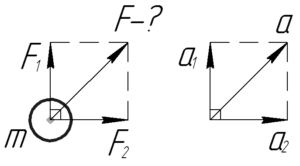Вы должны понимать, что материальная точка двигалась бы только с ускорением \(a_1\), если бы на тело действовала бы только сила \(F_1\) согласно принципу независимости действия сил (принципу суперпозиции). Также ускорение \(a_1\) можно интерпретировать как ускорение вдоль оси, сонаправленной с силой \(F_1\). Аналогично и с ускорением \(a_2\).
Так как на тело действуют две силы, то результирующую (равнодействующую) силу можно найти из второго закона Ньютона:
\[F = ma\]
Здесь \(a\) – суммарное ускорение мат. точки, которое можно найти по теореме Пифагора:
\[a = \sqrt {a_1^2 + a_2^2} \]
В итоге, решение задачи в общем виде выглядит так:
\[F = m\sqrt {a_1^2 + a_2^2} \]
Численный ответ равен:
\[F = 1\sqrt {{3^2} + {4^2}} = 5\; Н\]
Ответ: 5 Н.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.1.89 Тело массы 2 кг движется с результирующим ускорением 5 м/с2 под воздействием
2.2.1 Через неподвижный блок перекинута нить с грузами массой 3 и 5 кг. С каким ускорением
2.2.2 Три груза массами m1=1 кг, m2=2 кг, m3=3 кг соединены легкими нитями, проходящими
По правилу параллелограмма F=F1+F2
Можно записать, что F=ma1+ma2= 3+4=7
Ваше решение было бы правильным, если векторы ускорений a1 и a2 были коллинеарны и сонаправлены. Но это не так, они перпендикулярны друг другу, значит надо использовать правило параллелограмма и записать:
F=F1+F2
Здесь F1 и F2 – векторы, а не скаляры! Поскольку векторный треугольник – прямоугольный, то модуль вектора F можно найти по теореме Пифагора:
F=√(F1^2+F2^2)
F=√(m*a1^2+ma2^2)
F=m√(a1^2+a2^2)