Условие задачи:

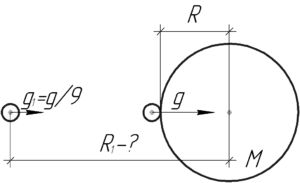
На каком расстоянии от центра Земли (в долях радиуса Земли \(R\)) ускорение свободного падения в 9 раз меньше, чем на поверхности Земли?

Задача №2.5.21 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(g_1=\frac{g}{9}\), \(R_1-?\)

Решение задачи:

Ускорение свободного падения на поверхности Земли \(g\) определяется по формуле:

\[g = G\frac{M}{{{R^2}}}\;\;\;\;(1)\]

На расстоянии \(R_1\) от центра Земли (учитывая, что \({R_1} > R\)) ускорение свободного падения \(g_1\) можно определить по формуле:

\[{g_1} = G\frac{M}{{R_1^2}}\;\;\;\;(2)\]

По условию \(g_1=\frac{g}{9}\), поэтому поделив выражение (1) на выражение (2), получим:

\[\frac{{R_1^2}}{{{R^2}}} = 9\]

\[\frac{{{R_1}}}{R} = 3\]

\[{R_1} = 3R\]

Многие на этом шаге закончили бы решение (как впрочем и я, до получения ценного комментария ниже) и записали бы ответ. Но на самом деле существует ещё одна точка (хотя правильно сказать ещё одно геометрическое место точек, отличное от уже полученного), в котором ускорение свободного падения в 9 раз меньше, чем на поверхности Земли. Оно находится внутри Земли!

Вообще ускорение свободного падения внутри (в толще) Земли \(g_1\) меняется по следующему закону (используя обозначения, принятые в нашей задаче):

\[g_1 = g\frac{R_1}{R}\]

Вывод этой закономерности оставим за рамками решения этой задачи.

Здесь \(g\) — ускорение свободного падения на поверхности Земли, \(R_1\) — расстояние от центра Земли до точки, в которой нужно найти ускорение свободного падения, \(R\) — радиус Земли.

Так как \(g_1=\frac{g}{9}\), то:

\[\frac{g}{9} = g\frac{{{R_1}}}{R}\]

\[\frac{{{R_1}}}{R} = \frac{1}{9}\]

\[{R_1} = \frac{1}{9}R\]

Вот теперь задача решена действительно полностью!

Ответ: \(\frac{1}{9}R\), \(3R\).

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

2.5.20 Радиус Земли равен 6400 км. Какую скорость имеют точки земной поверхности на широте
2.5.22 Радиус Земли равен 6400 км. На каком расстоянии от поверхности Земли сила притяжения
2.6.1 Для сжатия пружины на 2 см надо приложить силу 10 Н. Определить энергию упругой