Условие задачи:

На горизонтальной поверхности в 3 м от вертикальной стенки находится шар массой $M$. Другой шар массой $m$ скользит по направлению от стенки к шару $M$. После абсолютно упругого удара шар $m$ достигает стенки и, упруго отразившись от нее, догоняет шар $M$. Определить, на каком расстоянии от стенки произошло второе соударение, если $M/m=5$.

Задача №2.9.7 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

$l=3$ м, $M$, $m$, $\frac{M}{m}=5$, $L-?$

Решение задачи:

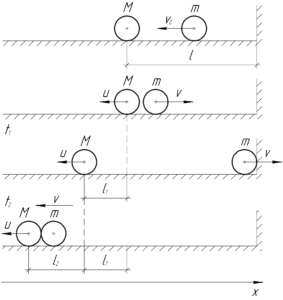Для начала разберемся с абсолютно упругим ударом шаров, то есть узнаем какие скорости шары приобретут после удара. Пусть изначально шар $m$ двигался со скоростью $\upsilon_0$ в направлении от стенки. После удара шар $m$ станет двигаться к стенке с некой скоростью $\upsilon$, а шар $M$ — от стенки со скоростью $u$.

Запишем закон сохранения импульса (ЗСИ) в проекции на ось $x$ и закон сохранения энергии (ЗСЭ):

$$\left\{ \begin{gathered} — m{\upsilon _0} = — Mu + m\upsilon \hfill \\ \frac{{m\upsilon _0^2}}{2} = \frac{{m{\upsilon ^2}}}{2} + \frac{{M{u^2}}}{2} \hfill \\ \end{gathered} \right.$$

ЗСИ перепишем в следующем виде:

$$m\left( {\upsilon  + {\upsilon _0}} \right) = Mu\;\;\;\;(1)$$

ЗСЭ запишем в таком виде, чтобы затем расписать разность квадратов:

$$\frac{m}{2}\left( {\upsilon _0^2 — {\upsilon ^2}} \right) = \frac{{M{u^2}}}{2}$$

$$\frac{m}{2}\left( {{\upsilon _0} + \upsilon } \right)\left( {{\upsilon _0} — \upsilon } \right) = \frac{{M{u^2}}}{2}$$

Учитывая (1), имеем:

$$\frac{{Mu}}{2}\left( {{\upsilon _0} — \upsilon } \right) = \frac{{M{u^2}}}{2}$$

$$u = {\upsilon _0} — \upsilon \;\;\;\;(2)$$

Полученное выражение для скорости шара $M$ подставим в (1).

$$m\left( {\upsilon  + {\upsilon _0}} \right) = M\left( {{\upsilon _0} — \upsilon } \right)$$

Попытаемся выразить скорость шара $m$ после удара:

$$m\upsilon  + m{\upsilon _0} = M{\upsilon _0} — M\upsilon$$

$$\upsilon \left( {m + M} \right) = {\upsilon _0}\left( {M — m} \right)$$

$$\upsilon  = \frac{{{\upsilon _0}\left( {M — m} \right)}}{{m + M}}$$

$$\upsilon  = \frac{{{\upsilon _0}\left( {\frac{M}{m} — 1} \right)}}{{1 + \frac{M}{m}}} = \frac{{{\upsilon _0}\left( {5 — 1} \right)}}{{1 + 5}} = \frac{2}{3}{\upsilon _0}$$

Используя равенство (2), получим:

$$u = {\upsilon _0} — \frac{2}{3}{\upsilon _0} = \frac{1}{3}{\upsilon _0}$$

Отлично, теперь можно заняться кинематикой задачи. На оба шара вдоль оси $x$ не действуют силы, поэтому они будут двигаться равномерно. После удара, за то время $t_1$, что шар $m$ достигнет стенки, шар $M$ удалится от своего первоначального положения на расстояние $l_1$. Будет правильно записать такую систему:

$$\left\{ \begin{gathered} l = \upsilon {t_1} \hfill \\ {l_1} = u{t_1} \hfill \\ \end{gathered} \right.$$

Поделим верхнее выражение этой системы на нижнее, получим:

$$\frac{l}{{{l_1}}} = \frac{\upsilon }{u}$$

Выше мы уже определили, что $u = \frac{1}{3}{\upsilon _0}$ и $\upsilon = \frac{2}{3}{\upsilon _0}$, значит:

$$\frac{l}{{{l_1}}} = \frac{{2{\upsilon _0} \cdot 3}}{{3{\upsilon _0}}} = 2$$

$${l_1} = \frac{1}{2}l$$

Далее шар $m$ упруго отскакивает от стенки и догоняет за время $t_2$ шар $M$, который пройдет дополнительно расстояние $l_2$. Понятно, что шар $m$ после удара о стенку пройдет искомое расстояние $L$. Запишем следующую систему:

$$\left\{ \begin{gathered} L = \upsilon {t_2} \hfill \\ {l_2} = u{t_2} \hfill \\ \end{gathered} \right.$$

Выполним аналогичные действия и получим:

$$\frac{L}{{{l_2}}} = 2$$

$${l_2} = \frac{1}{2}L$$

Из приведенного рисунка видно, что:

$$L = l + {l_1} + {l_2}$$

Так как мы уже знаем, что ${l_1} = \frac{1}{2}l$ и ${l_2} = \frac{1}{2}L$, то:

$$L = l + \frac{1}{2}l + \frac{1}{2}L$$

$$\frac{1}{2}L = \frac{3}{2}l$$

$$L = 3l$$

Посчитаем ответ:

$$L = 3 \cdot 3 = 9\; м$$

Ответ: 9 м.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

2.9.6 Шарик подлетает к неподвижной вертикальной стенке сверху со скоростью 10 м/с
2.10.1 По абсолютно гладкой поверхности движется со скоростью 6 м/с ящик с песком
2.10.2 Тележка массой 100 кг движется со скоростью 2 м/с. Когда она проезжает мимо