Условие задачи:

На горизонтальной плоскости сделан выстрел из винтовки, ствол которой направлен под углом 30° к плоскости. Пуля массой 10 г попала в вагончик массой 2 кг, шедший со скоростью 1 м/с навстречу пуле. Определите скорость вагончика после удара пули, если известно, что в момент удара расстояние между вагончиком и винтовкой 100 м и что конец ствола и вагончик находятся на одном уровне.

Задача №2.10.34 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(\alpha=30^\circ\), \(m=10\) г, \(M=2\) кг, \(\upsilon_1=1\) м/с, \(S=100\) м, \(u-?\)

Решение задачи:

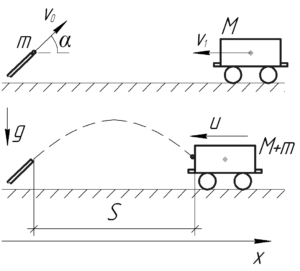На систему «пуля — вагончик» не действуют горизонтальные силы, значит импульс системы вдоль оси \(x\) должен оставаться постоянным по закону сохранения импульса:

\[m{\upsilon _0}\cos \alpha  — M{\upsilon _1} =  — \left( {M + m} \right)u\]

Выразим искомую скорость вагончика \(u\) после удара пули:

\[u = \frac{{M{\upsilon _1} — m{\upsilon _0}\cos \alpha }}{{M + m}}\;\;\;\;(1)\]

Если в момент удара расстояние между вагончиком и винтовкой равно \(S\), то именно это расстояние преодолела пуля по горизонтали. Так как конец винтовки и место удара пули о вагончик находится на одном уровне, то это расстояние можно записать в виде такой формулы:

\[S = {\upsilon _0}\cos \alpha  \cdot 2t\;\;\;\;(2)\]

Здесь \(t\) — это время подъема пули до наивысшей точки своей траектории, которую можно определить по формуле:

\[t = \frac{{{\upsilon _0}\sin \alpha }}{g}\]

Тогда (2) примет вид:

\[S = {\upsilon _0}\cos \alpha  \cdot 2\frac{{{\upsilon _0}\sin \alpha }}{g} = \frac{{\upsilon _0^2 \cdot \sin 2\alpha }}{g}\]

Выразим из последней формулы начальную скорость пули \(\upsilon_0\):

\[{\upsilon _0} = \sqrt {\frac{{gS}}{{\sin 2\alpha }}} \;\;\;\;(3)\]

Подставим (3) в (1), тем самым мы будем иметь решение задачи в общем виде:

\[u = \frac{{M{\upsilon _1} — m\sqrt {\frac{{gS}}{{\sin 2\alpha }}} \cos \alpha }}{{M + m}}\]

Переведем массу пули из грамм в килограммы, потом будем считать ответ:

\[10\; г = \frac{{10}}{{1000}}\; кг = 0,01\; кг\]

\[u = \frac{{2 \cdot 1 — 0,01\sqrt {\frac{{10 \cdot 100}}{{\sin 60^\circ }}} \cos 30^\circ }}{{2 + 0,01}} = 0,85\; м/с = 3,06\; км/ч\]

Ответ: 3,06 км/ч.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

2.10.33 Космический корабль на скорости 10 км/с попадает в неподвижное облако
2.10.35 С незакрепленной горки (клина) массой 1 кг соскальзывает тело массой 500 г. Угол
2.10.36 Снаряд, выпущенный из пушки под углом 45 градусов к горизонту, разрывается