Условие задачи:
На горизонтально расположенном диске, вращающемся с частотой 60 об/мин, помещают небольшой предмет. Максимальное расстояние предмета до оси вращения, при котором предмет удерживается на диске, равно 5,1 см. Чему равен коэффициент трения между предметом и диском?
Задача №2.4.38 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(\nu=60\) об/мин, \(R=5,1\) см, \(\mu-?\)
Решение задачи:
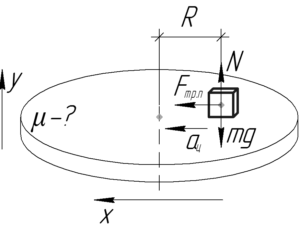 Вообще, на покоящийся относительно диска предмет действуют три силы: сила тяжести \(mg\), сила реакции опоры \(N\) и сила трения покоя \(F_{тр.п}\). Причем на расстоянии \(R\) от оси вращения сила трения покоя достигает своего максимального значения, поэтому её следует находить по формуле:
Вообще, на покоящийся относительно диска предмет действуют три силы: сила тяжести \(mg\), сила реакции опоры \(N\) и сила трения покоя \(F_{тр.п}\). Причем на расстоянии \(R\) от оси вращения сила трения покоя достигает своего максимального значения, поэтому её следует находить по формуле:
\[{F_{тр.п}} = \mu N\]
Силу реакции опоры найдем из первого закона Ньютона в проекции на ось \(y\):
\[N = mg\]
\[{F_{тр.п}} = \mu mg\;\;\;\;(1)\]
Второй закон Ньютона в проекции на ось \(x\) даст следующее равенство:
\[{F_{тр.п}} = m{a_ц}\]
Используя следующие известные формулы из кинематики вращательного движения, выразим центростремительное ускорение \(a_ц\) через частоту вращения диска:
\[{a_ц} = {\omega ^2}R\]
\[\omega = 2\pi \nu \]
Получим:
\[{a_ц} = 4{\pi ^2}{\nu ^2}R\]
\[{F_{тр.п}} = 4{\pi ^2}{\nu ^2}mR\;\;\;\;(2)\]
Из (1) и (2) следует, что:
\[\mu mg = 4{\pi ^2}{\nu ^2}mR\]
\[\mu = \frac{{4{\pi ^2}{\nu ^2}R}}{g}\]
Переведем частоту вращения \(\nu\) и расстояние \(R\) в систему СИ, потом уже подставим числа в дробь для расчета ответа.
\[60\; об/мин = \frac{{60}}{{60}}\; Гц = 1\; Гц\]
\[5,1\; см = \frac{{5,1}}{{100}}\; м = 0,051\; м\]
\[\mu = \frac{{4 \cdot {{3,14}^2} \cdot {1^2} \cdot 0,051}}{{10}} = 0,2\]
Ответ: 0,2.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.4.37 Тело массой 0,1 кг вращается в вертикальной плоскости на нити длиной 1 м. Ось
2.4.39 На конце стержня длиной 10 см укреплен груз массы 0,4 кг, приводимый во вращение
2.4.40 Бусинка может скользить вдоль гладкого кольца радиуса R, расположенного