Условие задачи:

Мяч падает с высоты 7,5 м на гладкий пол. Какую скорость нужно сообщить мячу, чтобы после двух ударов о пол он поднялся до первоначальной высоты, если при каждом ударе мяч теряет 40% энергии?

Задача №2.8.35 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(H=7,5\) м, \(\alpha=40\)%, \(\upsilon_0-?\)

Решение задачи:

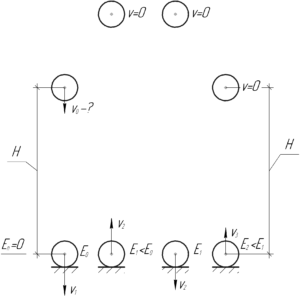Если следовать условию задачи, то в начальный момент полная механическая энергия мяча \(E_0\) состоит из потенциальной энергии \(mgH\) и кинетической энергии \(\frac{m\upsilon_0^2}{2}\).

\[{E_0} = mgH + \frac{{m\upsilon _0^2}}{2}\;\;\;\;(1)\]

Если после удара теряется \(\alpha\) процентов энергии, то остается — \(\left( {1 — \alpha } \right)\) процентов. Тогда полная механическая энергия после первого удара равна:

\[{E_1} = \left( {1 — \alpha } \right){E_0}\;\;\;\;(2)\]

После второго удара:

\[{E_2} = \left( {1 — \alpha } \right){E_1}\]

Учитывая формулы (1) и (2), имеем:

\[{E_2} = {\left( {1 — \alpha } \right)^2}\left( {mgH + \frac{{m\upsilon _0^2}}{2}} \right)\]

В конце концов мяч опять достигнет начальной высоты \(H\). Так как потерь энергии в процессе полета нет, то верно следующее:

\[{E_2} = mgH\]

Таким образом:

\[{\left( {1 — \alpha } \right)^2}\left( {mgH + \frac{{m\upsilon _0^2}}{2}} \right) = mgH\]

В этом уравнении одно неизвестное — искомая скорость \(\upsilon_0\). Произведем алгебраические преобразования, чтобы найти её:

\[{\left( {1 — \alpha } \right)^2}mgH + {\left( {1 — \alpha } \right)^2}\frac{{m\upsilon _0^2}}{2} = mgH\]

\[{\left( {1 — \alpha } \right)^2}2gH + {\left( {1 — \alpha } \right)^2}\upsilon _0^2 = 2gH\]

\[{\left( {1 — \alpha } \right)^2}\upsilon _0^2 = 2gH\left( {1 — {{\left( {1 — \alpha } \right)}^2}} \right)\]

\[{\upsilon _0} = \sqrt {\frac{{2gH\left( {1 — {{\left( {1 — \alpha } \right)}^2}} \right)}}{{{{\left( {1 — \alpha } \right)}^2}}}} \]

Разделим почленно дробь под знаком корня, тогда мы получим решение задачи в общем виде:

\[{\upsilon _0} = \sqrt {2gH\left( {\frac{1}{{{{\left( {1 — \alpha } \right)}^2}}} — 1} \right)} \]

Посчитаем численный ответ к задаче (проценты подставляем в долях единицы):

\[{\upsilon _0} = \sqrt {2 \cdot 10 \cdot 7,5\left( {\frac{1}{{{{\left( {1 — 0,4} \right)}^2}}} — 1} \right)}  = 16,33\; м/с = 58,79\; км/ч\]

Ответ: 58,79 км/ч.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

2.8.34 Шарик подбросили вверх, сообщив ему кинетическую энергию 20 Дж. Через
2.8.36 Тело, брошенное с вышки высотой 10 м, упало на землю со скоростью 15 м/с
2.8.37 Мяч скатился с горы высотой 20 м и после короткого горизонтального участка упал