Условие задачи:

Мотоциклист движется по цилиндрической стенке диаметра 12 м. При каком коэффициенте трения между стеной и колесами мотоцикла возможно движение со скоростью 54 км/ч?

Задача №2.4.32 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

$D=12$ м, $\upsilon=54$ км/ч, $\mu-?$

Решение задачи:

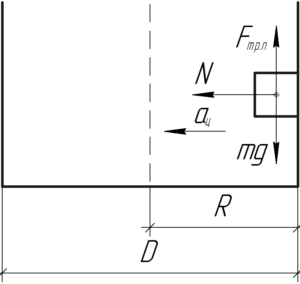На мотоциклиста действуют 3 силы: сила тяжести $mg$, сила реакции опоры $N$ и сила трения покоя $F_{тр.п}$, которая не дает ему соскользнуть вниз (смотрите схему).

Минимальный коэффициент трения $\mu$, при котором возможно такое движение, имеет место, когда сила трения покоя принимает максимальное значение. Как известно, в этом случае сила трения покоя уже равна силе трения скольжения, но тело ещё не проскальзывает. Поэтому:

$${F_{тр.п}} = \mu N\;\;\;\;(1)$$

Первый закон Ньютона в проекции на ось $y$ дает такое равенство:

$${F_{тр.п}} = mg\;\;\;\;(2)$$

Запишем также второй закон Ньютона в проекции на ось$x$:

$$N = m{a_ц}$$

Как известно, радиус цилиндра равен половине его диаметра $R=\frac{D}{2}$. Учитывая, что скорость мотоцикла равна $\upsilon$, то центростремительное ускорение $a_ц$ найдем по формуле:

$${a_ц} = \frac{{{\upsilon ^2}}}{R} = \frac{{2{\upsilon ^2}}}{D}$$

$$N = \frac{{2m{\upsilon ^2}}}{D}$$

Полученное подставим в (1), тогда:

$${F_{тр.п}} = \frac{{2\mu m{\upsilon ^2}}}{D}$$

Приравняем с (2), получим:

$$\frac{{2\mu m{\upsilon ^2}}}{D} = mg$$

$$\frac{{2\mu {\upsilon ^2}}}{D} = g$$

$$\mu  = \frac{{gD}}{{2{\upsilon ^2}}}$$

Переведем скорость в систему СИ:

$$54\; км/ч = \frac{{54 \cdot 1000}}{{1 \cdot 3600}}\; м/с = \frac{{540}}{{36}}\; м/с = 15\; м/с$$

Считаем ответ:

$$\mu  = \frac{{10 \cdot 12}}{{2 \cdot {{15}^2}}} = 0,27$$

Ответ: 0,27.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

2.4.31 Маленький шарик, подвешенный на нити, движется по окружности так, что нить
2.4.33 Спортивный молот — ядро на тросике длиной L, бросают, раскрутив вокруг себя
2.4.34 Тележка, скатившаяся по наклонному желобу с высоты 10 м, описывает в вертикальной