Ледяная горка составляет с горизонтом угол 10 градусов. По ней пускают вверх камень

Условие задачи:

Ледяная горка составляет с горизонтом угол 10°. По ней пускают вверх камень, который, поднявшись на некоторую высоту, соскальзывает по тому же пути вниз. Каков коэффициент трения, если время спуска в 2 раза больше времени подъема?

Задача №2.3.14 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(\alpha=10^\circ\), \(\tau=2t\), \(\mu-?\)

Решение задачи:

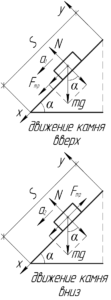Рассмотрим движение камня вверх по горке. Пусть у основания горки камень имеет скорость \(\upsilon_0\). Двигаясь равнозамедленно с ускорением \(a_1\) он пройдёт за время \(t\) расстояние \(S\) и остановится. Формула скорости камня при этом такая:

\[0 = {\upsilon _0} – {a_1}t\]

\[{\upsilon _0} = {a_1}t\;\;\;\;(1)\]

Также применим такую известную формулу из кинематики:

\[0 – \upsilon _0^2 =  – 2{a_1}S\]

Используя выражение (1), получим:

\[a_1^2{t^2} = 2{a_1}S\]

\[t = \sqrt {\frac{{2S}}{{{a_1}}}} \;\;\;\;(2)\]

Запишем второй закон Ньютона в проекции на ось \(x\) и первый закон Ньютона в проекции на ось \(y\), тогда:

\[\left\{ \begin{gathered}
mg \cdot \sin \alpha + {F_{тр}} = m{a_1} \hfill \\
N = mg \cdot \cos \alpha \hfill \\
\end{gathered} \right.\]

Определить силу трения просто, достаточно вспомнить такую формулу:

\[{F_{тр}} = \mu N\]

\[{F_{тр}} = \mu mg \cdot \cos \alpha \]

Первое равенство системы примет такой вид:

\[mg \cdot \sin \alpha  + \mu mg \cdot \cos \alpha  = m{a_1}\]

\[{a_1} = g\sin \alpha  + \mu g\cos \alpha \]

Формула (2) для времени подъема станет уже такой:

\[t = \sqrt {\frac{{2S}}{{g\sin \alpha  + \mu g\cos \alpha }}} \;\;\;\;(3)\]

Перейдем к движению камня вниз. Очевидно, что он скользит без начальной скорости с ускорением \(a_2\), запишем такое уравнение движения:

\[S = \frac{{{a_2}{\tau ^2}}}{2}\]

\[\tau  = \sqrt {\frac{{2S}}{{{a_2}}}} \;\;\;\;(4)\]

Аналогично записываем законы Ньютона в проекции на оси координат:

\[\left\{ \begin{gathered}
mg \cdot \sin \alpha – {F_{тр}} = m{a_2} \hfill \\
N = mg \cdot \cos \alpha \hfill \\
\end{gathered} \right.\]

Сила трения определяется аналогично, поэтому опустим этот момент. Ускорение \(a_2\) равно:

\[{a_2} = g\sin \alpha  – \mu g\cos \alpha \]

Формула (4) для времени спуска получается такой:

\[\tau  = \sqrt {\frac{{2S}}{{g\sin \alpha  – \mu g\cos \alpha }}} \;\;\;\;(5)\]

Отношение время спуска \(\tau\) ко времени подъема \(t\) равно двум по условию, поэтому, поделив выражение (5) на выражение (3), получим:

\[\sqrt {\frac{{\sin \alpha  + \mu \cos \alpha }}{{\sin \alpha  – \mu \cos \alpha }}}  = 2\]

Возводим в квадрат, далее перемножаем “крест-накрест”.

\[\frac{{\sin \alpha  + \mu \cos \alpha }}{{\sin \alpha  – \mu \cos \alpha }} = 4\]

\[\sin \alpha  + \mu \cos \alpha  = 4\sin \alpha  – 4\mu \cos \alpha \]

\[5\mu \cos \alpha  = 3\sin \alpha \]

\[\mu  = \frac{3}{5}tg\alpha \]

Мы решили задачу в общем виде, теперь посчитаем ответ:

\[\mu  = \frac{3}{5}tg10^\circ  = 0,106\]

Ответ: 0,106.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

2.3.13 Ледяная гора составляет с горизонтом угол 30 градусов, по ней снизу вверх пускают
2.3.15 С каким ускорением движутся грузы m1=0,5 кг и m2=0,6 кг, если высота наклонной
2.3.16 С горы высотой 2 м и основанием 5 м съезжают санки, которые затем останавливаются