Ледяная гора составляет с горизонтом угол 30 градусов, по ней снизу вверх пускают

Условие задачи:

Ледяная гора составляет с горизонтом угол 30°, по ней снизу вверх пускают камень, который в течение 2 с проходит расстояние 16 м, после чего соскальзывает вниз. Сколько времени длится соскальзывание камня вниз?

Задача №2.3.13 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(\alpha=30^\circ\), \(t=2\) с, \(S=16\) м, \(\tau-?\)

Решение задачи:

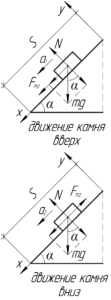Решать задачу будем с конца. Понятно, что вниз камень будет двигаться без начальной скорости с некоторым ускорением \(a_2\). При этом он пройдёт расстояние \(S\), поэтому искомое время \(\tau\) следует искать из уравнения движения камня вдоль оси \(x\):

\[S = \frac{{{a_2}{\tau ^2}}}{2}\]

\[\tau  = \sqrt {\frac{{2S}}{{{a_2}}}} \;\;\;\;(1)\]

Ускорение камня при движении вниз найдем из второго закона Ньютона, записанного в проекции на ось \(x\):

\[mg \cdot \sin \alpha  – {F_{тр}} = ma_2\]

Силу трения скольжения \(F_{тр}\) определим по такой формуле:

\[{F_{тр}} = \mu N\]

Реакцию опоры \(N\) можно определить по первому закону Ньютона, записанного в проекции на ось \(y\):

\[N = mg \cdot \cos \alpha \]

Тогда:

\[{F_{тр}} = \mu mg \cdot \cos \alpha \]

\[mg \cdot \sin \alpha  – \mu mg \cdot \cos \alpha  = ma_2\]

\[{a_2} = g\left( {\sin \alpha  – \mu \cos \alpha } \right)\]

Отлично, мы нашли ускорение \(a_2\). Формула (1) примет вид:

\[\tau  = \sqrt {\frac{{2S}}{{g\left( {\sin \alpha  – \mu \cos \alpha } \right)}}} \;\;\;\;(2)\]

Нам неизвестен коэффициент трения \(\mu\). Мы найдем его, рассмотрев движения камня вверх по горке. Имея некоторую начальную скорость у основания \(\upsilon_0\), камень будет двигаться по горке равнозамедленно с ускорением \(a_1\) в течение времени \(t\). Он пройдет расстояние \(S\) по горке. Формула скорости для камня:

\[0 = {\upsilon _0} – {a_1}t\]

\[{\upsilon _0} = {a_1}t\;\;\;\;(3)\]

Также применим такую формулу из кинематики:

\[0 – \upsilon _0^2 =  – 2{a_1}S\]

Учитывая ранее полученное выражение (3), имеем:

\[ – a_1^2{t^2} =  – 2{a_1}S\]

\[{a_1} = \frac{{2S}}{{{t^2}}}\;\;\;\;(4)\]

Опять применим второй закон Ньютона в проекции на ось \(x\), опустив нахождение силы трения, так как оно в этом случае такое же, как и выше.

\[mg \cdot \sin \alpha  + \mu mg \cdot \cos \alpha  = m{a_1}\]

\[{a_1} = g\sin \alpha  + \mu g\cos \alpha \]

Приравняем полученное с (4) и выразим произведение \(\mu \cos \alpha\).

\[\frac{{2S}}{{{t^2}}} = g\sin \alpha  + \mu g\cos \alpha \]

\[\mu \cos \alpha  = \frac{{2S}}{{g{t^2}}} – \sin \alpha \]

Полученное выражение подставим в (2) и, произведя преобразования, получим такое решение:

\[\tau  = t\sqrt {\frac{S}{{g{t^2}\sin \alpha  – S}}} \]

Осталось только посчитать ответ:

\[\tau  = 2\sqrt {\frac{{16}}{{10 \cdot {2^2} \cdot \sin 30^\circ  – 16}}}  = 4\; с\]

Ответ: 4 с.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

2.3.12 Брусок сползает без начальной скорости с высоты 2 м по доске, наклоненной
2.3.14 Ледяная горка составляет с горизонтом угол 10 градусов. По ней пускают вверх камень
2.3.15 С каким ускорением движутся грузы m1=0,5 кг и m2=0,6 кг, если высота наклонной