Условие задачи:
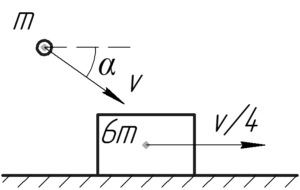Кусок пластилина массой \(m=32\) г попадает в брусок массой \(6m\), двигавшийся по гладкой горизонтальной поверхности стола, и прилипает к нему. Перед ударом скорость пластилина равна \(\upsilon=7\) м/с и направлена под углом \(\alpha=60^\circ\) к горизонту, а скорость бруска равна \(\upsilon/4\). Определить скорость бруска с пластилином после удара.
Задача №2.10.20 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(m=32\) г, \(6m\), \(\upsilon=7\) м/с, \(\alpha=60^\circ\), \(\upsilon/4\), \(u-?\)
Решение задачи:
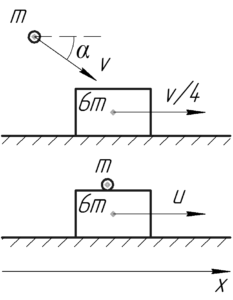На брусок и пластилин не действуют никакие горизонтальные силы, значит суммарный импульс обоих тел в проекции на ось \(x\) будет сохраняться согласно закону сохранения импульса. Запишем его для моментов до и после удара (в проекции на ось \(x\)):
\[m\upsilon \cdot \cos \alpha + 6m \cdot \frac{\upsilon }{4} = \left( {m + 6m} \right)u\]
Сократим обе части равенства на \(m\), тогда:
\[\upsilon \cdot \cos \alpha + 1,5\upsilon = 7u\]
Искомая скорость бруска с пластилином \(u\) после слипания равна:
\[u = \frac{{\upsilon \cdot \cos \alpha + 1,5\upsilon }}{7}\]
\[u = \frac{{\upsilon \left( {\cos \alpha + 1,5} \right)}}{7}\]
Посчитаем ответ к задаче:
\[u = \frac{{7\left( {\cos 60^\circ + 1,5} \right)}}{7} = 2\; м/с = 7,2\; км/ч\]
Ответ: 7,2 км/ч.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.10.19 Конькобежец, стоя на льду, бросает горизонтально с высоты 1,5 м груз массой 10 кг
2.10.21 На горизонтальном столе лежит деревянный брусок массой 5 кг. В брусок попадает
2.10.22 По горизонтальной поверхности стола скользит брусок массой m и сталкивается